Simulación de Sistemas Dinámicos Usando Software de Código Abierto
Domingo Cortés, Diego Martínez, Bryan Parra
1. Introducción
En este documento se presenta como simular sistemas dinámicos usando software de código abierto disponible gratuitamente en la internet.
Es común que estudiantes y profesionistas recurran automáticamente a MatLab cuando necesitan simular sistemas dinámicos. Sin embargo, por su costo, MatLab es cada vez es menos disponibles en instituciones educativas, por otra parte, las bibliotecas de funciones existentes en software de código abierto son más poderosas y eficientes. Es esta combinación de factores que dio origen a este documento.
2. Tutorial de simulación en Xppaut
2.1. Descripción de Xppaut
Xppaut es un software para (entre otras cosas) simular sistemas dinámicos descritos por ecuaciones diferenciales. Para simular sistemas en Xppaut se describen las ecuaciones diferenciales en un archivo de texto y se abre con Xppaut.
Suponga que el archivo donde está descrito el sistema se llama ecuaciones.ode. Para simular el sistema:
- En windows se arrastra este archivo y se coloca encima del ejecutable; eso abrirá Xppaut y cargará el archivo ecuaciones.ode.
- En Linux se puede ejecutar desde la consola
xppaut ecuaciones.ode
Se acostumbra poner la extensión .ode a los archivos de texto que describen sistemas en xppaut; esto para indicar que al archivo describe una Ordinary Differential Equation.
2.2. Instalación de Xppaut
Xppaut puede descargarse desde la pagina xppaut/descarga tanto en su versión para Linux como para windows.
2.3. Descripción de un sistema en Xppaut
La descripción de las ecuaciones diferenciales se hace mediante una representación simple. Los elementos básicos son los siguientes
2.3.1. Especificación de un sistema de primer orden
Para simular el sistema de primer orden \[ \dot x = ax + bu \] dónde \(a\) y \(b\) son constantes y \(u\) es una función del tiempo se introduce:
dx/dt=a*x+b*u
de manera más corta también se puede usar:
x'= a*x + b*u
2.3.2. Especificación de los parámetros
Los valores constantes en un sistema se conocen como parámetros del sistema. En el sistema que se quiere simular \(a\) y \(b\) son los parámetros del sistema; para efectuar una simulación es necesario conocer el valor de estos parámetros. El valor de los parámetros, en Xppaut se especifica con param o más simple par de la siguiente manera
par a=-1, b=3
2.3.3. Funciones del tiempo
En el sistema que se quiere simular \(u\) es una función del tiempo. Supongamos que queremos que \(u=3+2sen(0.5t)\) esto se introduce en Xppaut como:
u=3+2*sin(0.5*t)
En Xppaut cualquier línea que tenga el patrón
var=expr(t)
hace que var sea una función del tiempo. Xppaut incluye una amplia variedad de funciones predefinidas que se pueden combinar para formar nuevas expresiones.
2.3.4. Especificación de las condiciones iniciales
Para especificar la condición inicial \(x(0)=1\) se escribe tal cual.
x(0)=1
O bien
init x=1
de esta última forma se pueden especificar más de una condición inicial en una sola línea.
2.3.5. Comentarios
Los comentarios sirven para documentar un sistema; es decir para recordarnos cosas del sistema y su simulación. Por ejemplo, nos pueden recordar el objetivo del sistema, lo que significa cada variable, la fecha en que se creó el archivo, etc.
Xppaut ignora cualquier línea que empieza con `#', por ello se usan para introducir comentarios que quepan en una línea. Se pueden introducir comentarios más largos, poniendo `#' al inicio de cada línea. Por ejemplo:
# Curso de Sistemas no lineales # Modelo de un sistema rapaz-presa # Creado el 15 de agosto de 2010; ultima revision 30 sept. 2019
Xppaut también ignora todo lo que siga a una línea que sólo contenga el texto done; esto permite introducir una explicación amplia del sistema.
2.3.6. Definiendo las señales que se desea graficar
Por default, durante una simulación, Xppaut guarda las variables de estado; pero se puede especificar que guarde cualquier otra señal. Para ello se sigue el patrón:
aux nombre=señal
donde señal es el nombre de la señal que se desea almacenar y nombre es un alias con el que Xppaut conocerá a la señal. Por ejemplo si se quisiera guardar la señal \(u\) se podría agregar al archivo .ode la siguiente línea
aux control=u
De esta manera, en la sesión de Xppaut se podría graficar el control. El nombre control sólo se conoce en la sesión de Xppaut por lo que no se puede usar en las formulas del archivo .ode
2.3.7. Opciones de simulación.
Para efectuar una simulación es necesario especificar el tiempo de simulación, el método de integración el máximo paso de integración, etc. Además xppaut permite limitar el máximo número de datos que se almacenarán y un máximo para los valores que pueden tomar la variables en una simulación, etc. Cabe aclarar que la mayoría de estas opciones pueden cambiarse dentro de Xppaut. Sin embargo, es conveniente que se puedan especificar desde el archivo .ode pues facilita mucho la simulación, sobre todo, si el archivo .ode se va a usar más de una vez.
Para especificar las opciones se sigue el patrón
@ option1=valor @ option2=valor
o bien se pueden especificar varias en una sola línea separadas por comas
@ opcion1=valor, opcion2=valor, opcion3=valor
Por ejemplo para especificar un tiempo de simulación de 5, se usa:
@ total=5
Para especificar un paso de integración de 0.0001 se usa
@ dt=0.0001
La siguiente línea especifica que se guardarán un máximo de 5 millones de datos
@ MAXSTOR=5000000
La siguiente línea establece que si el valor absoluto de una variable excede \(10^{6}\) la simulación se detiene
@ BOUND=1e6
2.4. Un ejemplo completo de un archivo .ode
El siguiente archivo de texto describe una ecuación diferencial en xppaut
# Describiendo un sistema sencillo en xppaut x'= a*x + b*u # Valores de los parámetros par a=-1, b=3 # especificación de la señal 'u' u=3+2*sin(0.5*t) # Condición inicial: init x=1 # Le ponemos a 'u' el alias de 'control' para poder graficarlo aux control=u # Opciones de simulación @ total=5 @ dt=0.0001 @ MAXSTOR=5000000 @ BOUND=1e6 done Este archivo es un ejemplo completo de la especificación de un sistema en Xppaut guárdelo como ejemplo.ode y ábralo con Xppaut
2.5. Uso de Xppaut
2.5.1. Corregir los errores en caso de haberlos
Al abrir un archivo con Xppaut, éste examina si el archivo contiene un sistema con expresiones válidas; si no es así produce un error. Examine con mucho cuidado los mensajes de error que Xppaut produce porque pueden facilitar la corrección de errores.
Si los mensajes de error no son de utilidad revise cuidadosamente línea por línea del archivo.
Elimine las líneas que nos son vitales en la descripción del modelo; por ejemplo las líneas que empiezan con:
- aux
- init
- @
Una vez que el archivo se haya abierto sin problemas puede volver a agregarlas una por una.
2.5.2. La interfaz de Xppaut
La interfaz de Xppaut ya muestra sus años (ver figura 1), sin embargo, se puede seguir operando con el ratón. Sin embargo, es mucho más fácil operar Xppaut con el teclado cada vez que se pueda. Para operar Xppaut con el teclado, note que casi todos los botones tienen una letra mayúscula; esta letra identifica la tecla que hay que presionar para activar el botón.
Con el fin de ilustrar el uso de la interfaz de Xppaut, en lo que sigue se mencionan algunas combinaciones de teclas para realizar algunas tareas comunes. Sin embargo, para usar eficientemente la interfaz es necesario explorarla.
Muchos de los botones de la pantalla inicial de Xppaut abren submenus. Para volver al menú principal se puede teclear 'esc' o dar click en 'close'.
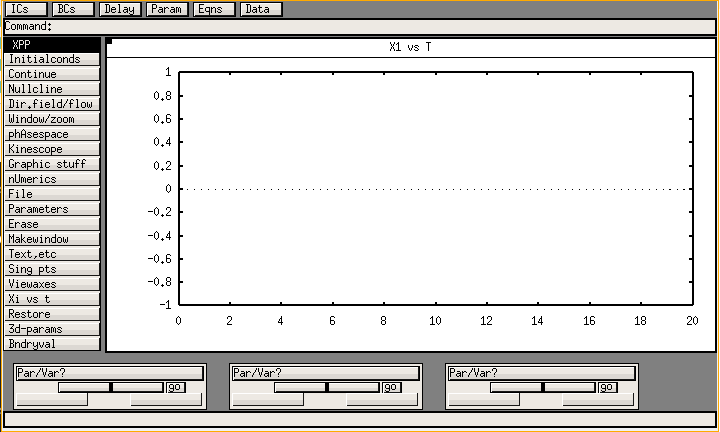
Figure 1: Interfaz principal de Xppaut
2.5.3. Salir de Xppaut
Para salir de Xppaut teclear: (F)ile -> (Q)uit -> (Y)es
2.5.4. Haciendo una simulación y graficando una variable
La tecla `I' accede al menú de integración (aunque por error Xppaut dice Initialconds; ver figura 2). En este menú hay varios submenús, algunos de los cuales se explican adelante. Por ahora para realizar una simulación teclee 'I' (Integración) y entonces 'G' (Go). La solución se mostrará en la ventana principal.
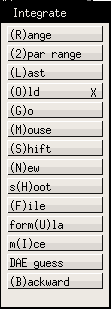
Figure 2: Menú Integrate
Teclee 'X' (Xi vs t) para graficar una señal; Xppaut pregunta que señal se quiere graficar, el default es la primera variable definida en el archivo .ode. Recuerde que solo se pueden graficar las variables de estado o las señales especificadas por aux.
2.5.5. Cambiando condiciones iniciales y parámetros
En la parte superior de la interfaz hay 6 botones que se tiene que activar con el mouse porque no les corresponde ninguna tecla. Nos interesan por ahora los que dicen 'ICs' y 'Param'. Estos botones sirven para cambiar las condiciones iniciales (c.i.) y los parámetros respectivamente. Note que hay que volver a integrar (simular) las ecuaciones para que la gráfica corresponda a los nuevos valores de c.i. y parámetros
En el caso de los parámetros éstos también se pueden cambiar tecleando 'p' desde el menú principal; en este caso Xppaut pregunta el nombre del parámetro y después su valor.
En el caso de las c.i. estas se pueden cambiar al iniciar una simulación como sigue:
- 'I' seguida de 'G' usa la c.i. actual y entonces integra
- 'I' seguida de 'N' pregunta por una nueva c.i. y entonces integra
- 'I' seguida de 'L' usa el valor final de la simulación anterior y entonces integra.
- 'I' seguida de 'R' abre un submenú donde se puede especificar un rango de condiciones iniciales para una variable de estado.
2.5.6. Examinando y guardando los datos
Uno de los seis botones de la parte superior dice 'Data'; este botón despliega los valores que adquirieron las variables durante la simulación. Hay varias acciones que se pueden realizar con los datos de simulación. Quizá la acción más útil es guardar los datos para graficarlos en un programa que ofrezca más flexibilidad para realizar gráficas. Esto se hace con el botón 'write'. Esto genera un archivo con la extensión '.dat' que contiene los datos de simulación en formato texto separados por espacio. Como el formato es texto simple, este archivo puede ser leído prácticamente por cualquier software.
2.5.7. Graficando variables
Las utilidades gráficas de Xppaut no son las mejores. Para resultados profesionales siempre es mejor guardar los datos y graficarlos en otro software. Sin embargo, Xppaut incluye capacidades gráficas para analizar los resultados de forma rápida y eficiente.
Las utilidades gráficas estás distribuidas en los menús
- (W)indow/zoom (ver figura 3)
- (W)Window: define los rangos de los ejes
- (Z)oom in: Hace un acercamiento con el mouse
- Zoom (O)ut: Hace un alejamiento
- (F)it: ajusta el rango de los ejes para que la(s) gráfica(s) quepan en la ventana.
- (D)efault: vuelve a la ventana por default
- (G)raphic stuff (ver figura 4): Agrega, remueve o congela (para que no se borren) curvas de una ventana. Desde este menú también se pueden exportar los datos
- (M)ake window: Crea o elimina ventanas que podrían ser usadas por ejemplo para poder ver distintas curvas en cada ventana.
- (V)iew axes (ver figura 5): En el submenú 2d (ver figura 6)se puede definir la curva graficada así como los rangos y etiquetas de los ejes.
- (X)i vs t: Pregunta por una variable de estado para graficarla.
Cuando se quiere desplegar más de una gráfica, usualmente se grafica de una variable de estado con '(X)i vs t' y después con 'Graphic stuff' se agregan el resto de las gráficas; si es necesario se ajustan los ejes con '(w)indow->(f)it' o bien con '(W)indow -> (W)indow'
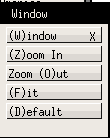
Figure 3: Menú Windows
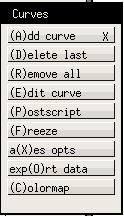
Figure 4: Menú Graphic stuff
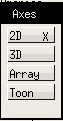
Figure 5: Menú View axes
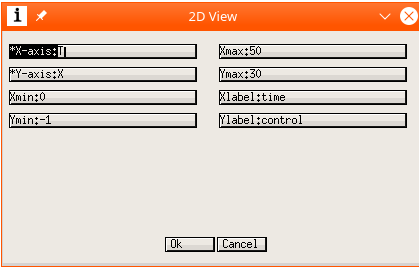
Figure 6: Menú View axes -> 2d view
2.5.8. Cambiando los parámetros de simulación
En el menú `n(U)merics' (ver figura 7) se pueden cambiar los parámetros de simulación (no del sistema) como el tiempo (T)otal de simulación, el paso de integración 'Dt', el tiempo inicial de simulación '(S)tart time', el método de integración '(M)ethod', etc.
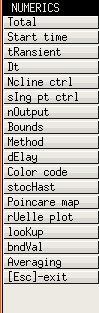
Figure 7: Menú nUmerics
2.6. Descripción del péndulo simple en Xppaut
En la figura 8 se muestra el diagrama de un péndulo simple. Aplicando las ecuaciones de Euler-Lagrange se puede obtener el siguiente modelo del sistema
\begin{equation} ml^{2} \ddot \theta + mglsen(\theta) + bl\dot \theta - \tau \end{equation}donde \(\theta\) es el ángulo del péndulo con respecto a la vertical, \(m\) es la masa del péndulo, \(l\) es su longitud, \(g\) la fuerza de gravedad, \(b\) la constante que determina la fricción en el pivote del péndulo y \(\tau\) es el par aplicado en el pivote del péndulo.
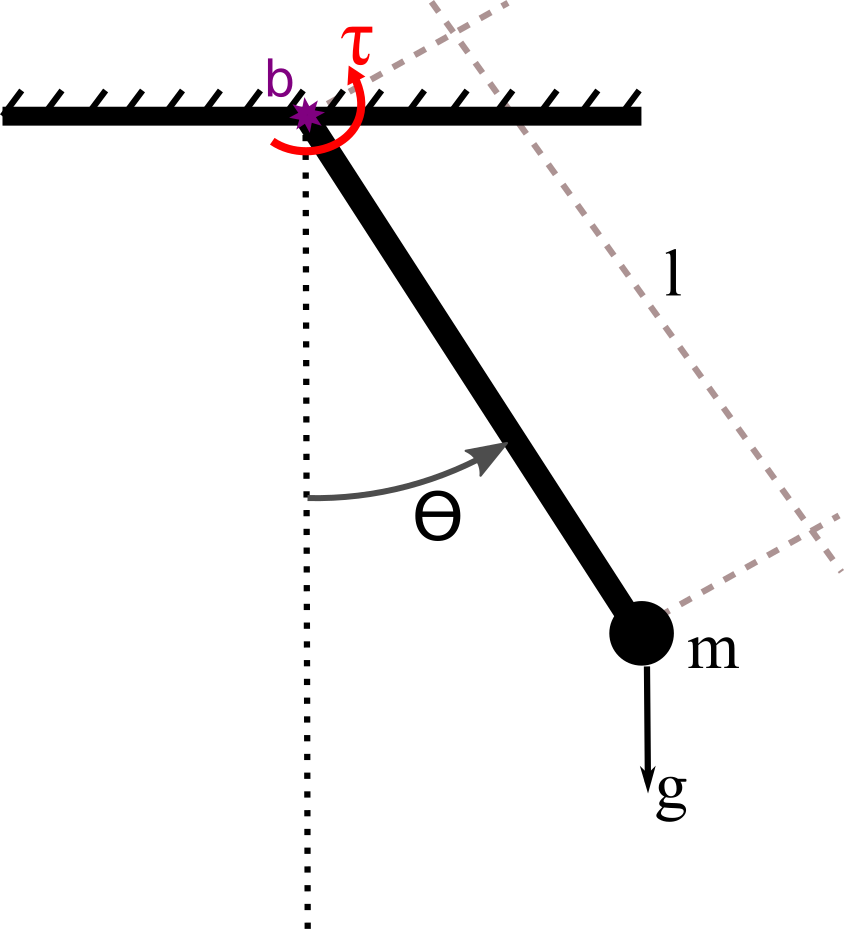
Figure 8: Diagrama del péndulo simple
Haciendo \(x_{1}=\theta\); \(x_{2}=\dot \theta\) se pueden obtener las siguientes ecuaciones de estado
\begin{align} \dot x_{1} &= x_{2} \\ \dot x_{2} &= -\frac{g}{l}\sin(x_{1})-\frac{b}{ml}x_{2} + \frac{\tau}{ml^{2}} \end{align}De acuerdo a las secciones previas, estas ecuaciones de estado se pueden simular en Xppaut mediante las líneas
# simulacion del péndulo simple # El modelo del péndulo x1'= x2 x2'= -(g/l)*sin(x1)-b*x2/(m*l) + tau/(m*l*l) # con los parámetros par g=9.8 m=0.3 l=0.5 b=0.1 # y la condición inicial init x1=pi/4 # y el par tau=0 done
3. Simulación de sistemas dinámicos continuos usando Python
3.1. Introducción
Aquí se presenta a través de ejemplos como simular un sistema dinámico en python. Aunque existen diversas bibliotecas que facilitan esta tarea, en este documento se busca usar el menor número de bibliotecas posible. Así, se usa extensivamente la función odeint de la biblioteca scipy.integrate para simular sistemas dinámicos. Se describe como simular sistemas en lazo abierto (autónomos) y en lazo cerrado (con control) con y sin perturbaciones. Como cambiar el intervalo de simulación y como cambiar las condiciones iniciales.
3.2. Simulación de sistemas de primer orden
Antes de presentar un ejemplo de como simular un sistema de primer orden es conveniente describir varias funciones útiles que están en distintas bibliotecas. En particular se requiere
- Varias funciones de la biblioteca numpy
- Las funciones de la biblioteca math
- La función odeint que está en la biblioteca scipy.integrate
- Las funciones de pyplot que están en la biblioteca matplotlib
La forma de importar las funciones necesarias depende de si se necesita toda la biblioteca o sólo una función. El código en Python para tener acceso a todas las funciones necesarias en los ejemplos que se describen más adelante, es:
import numpy as np import math from scipy.integrate import odeint import matplotlib.pyplot as plt
La forma más sencilla de usar odeint es resolver una ecuación de estado de primer orden. Para resolver la ecuación 'odeint' requiere que se especifiquen tres cosas:
- La ecuación de estado.
- La condición inicial.
- Una secuencia de tiempos en donde se desea la solución.
A partir de estos tres argumentos, odeint devuelve una secuencia de valores del estado en los tiempos especificados. Más concretamente odeint se usa así:
x = odeint(modelo,x_0,t)
donde modelo es la ecuación de estado, \(x_0\) es la condición inicial, \(t\) es una secuencia de valores de tiempo donde se desea conocer la solución y \(x\) es una secuencia de valores del estado para cada valor de \(t\). Por supuesto \(x\), modelo, \(x_0\) y \(t\) son nombres que podrían cambiar.
El modelo es una función que acepta el estado \(x\) y el tiempo \(t\) y devuelve el valor de la derivada \(xp\) para ese estado y tiempo. Por ejemplo, suponga que se desar simular el sistema
\begin{equation} \label{eq:1} \dot x = -k x + 1 \end{equation}con \(k=0.5\). En Python dicho sistema se describe así
def modelo(x,t): k = 0.5 xp = -k * x + 1 return xp
La secuencia de valores de tiempo donde se desea conocer la solución (el estado) se puede crear con linspace de numpy. Por ejemplo usando
t = np.linspace(0,10,101)
donde \((0,10,101)\) especifica una secuencia de \(101\) valores espaciados de manera uniforme con inicio en \(0\), terminación en \(10\).
Quizá llame la atención que se use \(101\) valores en lugar de \(100\). Esto es porque tanto el \(0\) como el \(100\) están incluidos en la secuencia. Así con \(101\) valores se obtiene la secuencia \([0, 0.1, 0.2, ... 10]\).
La condición inicial del estado \(x_0\) es este caso es un número. Por ejemplo:
x_0 = 0
Después de ejecutar odeint la solución se almacena como una secuencia en \(x\). Esta secuencia tiene el mismo tamaño que \(t\) por lo que se puede graficar \(x\) vs \(t\) usando las funciones de pyplot:
plt.plot(t,x) plt.xlabel('t') plt.ylabel('x(t)') plt.show()
El código completo resulta para la simulación del sistema \eqref{eq:1} en el intervalo \([0,10]\) resulta
import numpy as np import math from scipy.integrate import odeint import matplotlib.pyplot as plt # El modelo toma x y t actual y regresa xp = dx/dt def modelo(x,t): k = 0.5 xp = -k * x + 1 return xp x_0 = 0 t = np.linspace(0,10,101) # se obtiene la solución x = odeint(modelo,x_0,t) # Grafica los resultados plt.plot(t,x) plt.xlabel('t') plt.ylabel('x(t)') plt.show()
Note que se pueden simular modelos no lineales y variantes en el tiempo. Por ejemplo para simular el sistema
\begin{equation} \label{eq:2} \dot x = -k x^{3} + \sin(t) \end{equation}en Python habría que cambiar el código de la función modela a:
def modelo(x,t): k = 0.5 xp = -k * x*x*x + math.sin(t) return xp
3.3. Simulación de sistemas con control
Para simular sistemas controlados o con perturbaciones sólo es necesario que la función donde se especifica la ecuación de estado dependa de otras funciones. Consider por ejemplo, que se desea simular el sistema
\begin{equation} \label{eq:3} \dot x = -a*x + u(x) + p(t) \end{equation}donde \(a=0.1\), la ley de control \(u\) y la perturbación \(p\) están dadas por \(u(x)=kp(ref-x)\) y \(p(t)=b \sin(w t)\) respectivamente. El código para simular este sistema es
def modelo(x,t): a = 0.1 xp = -a*x + u(x,t) + p(x,t) return xp
Note que la función modelo depende de las funciones \(u(x)\) y \(p(t)\) que corresponden al control y a la perturbación y que podrían codificarse en Python así:
def u(x): kp = 1 ref = 1 error = (ref-x) control = kp*error return control def p(t): w = 100 b = 0.5 perturbacion = b*math.sin(w*t) return perturbacion
La secuencia de tiempos en donde se desea la solución se puede generar en base al tiempo inicial, el tiempo final y el espacio entre muestra como se describe en el siguiente código
t_ini = 0 #t inicial t_fin = 10 #t final t_step = 0.1 #tamaño del paso n_m = (t_fin - t_ini)/t_step +1 #numero de muestras t = np.linspace(t_ini,t_fin,n_m)
Al igual que antes para generar la secuencia se necesita el inicio, el final y el número de muestras; sin embargo, ahora estos datos se introducen a partir de variables que tienen más significado para quien este simulando.
El código completo de la simulación del sistema de primer orden dado por \eqref{eq:3} con control y perturbación queda
import numpy as np import math from scipy.integrate import odeint import matplotlib.pyplot as plt # El modelo x y t actual y regresa xp = dx/dt def modelo(x,t): a = 0.1 xp = -a*x + u(x) + p(t) return xp # El control u(x) def u(x): kp = 1 ref = 1 error = (ref-x) control = kp*error return control # La perturbación p(t) def p(t): w = 100 b = 0.5 perturbacion = b*math.sin(w*t) return perturbacion # Condición inicial x_0 = 0 # Genera la secuencia de tiempo t_ini = 0 #t inicial t_fin = 10 #t final t_step = 0.1 #espaciado n_m = (t_fin - t_ini)/t_step +1 #numero de muestras t = np.linspace(t_ini,t_fin,n_m) # obtiene la solución x = odeint(modelo,x_0,t) # Grafica los resultados plt.plot(t,x) plt.xlabel('t') plt.ylabel('x(t)') plt.show()
3.4. Simulación de sistemas de orden 2 o más
En sistemas de orden 2 o superior el estado del sistema es un vector. En Python el vector de estados se puede representar como una lista de números. Si se hace así el uso de 'odeint' no cambia, es exactamente como antes:
x = odeint(modelo,x_0,t)
Lo que cambia es que modelo debe aceptar un vector de estado y devolver un vector de valores para la derivada. Ambos vectores se representarán como listas. De la misma manera si el sistem incluye un término de control, la función del control debe recibir el vector de estados y devolver el cálculo del control. Dado que el estado es ahora un vector, la condición inicial tambien es un vector.
Como ejemplo concreto suponga que se desea simular el sistema
\begin{equation} \begin{aligned} \dot x_{1} &= -k_{1} x_{1} -1 + u(x,t) \\ \dot x_{2} &= -k_{2} x_{2} -1.5 + u(x,t) \end{aligned} \label{eq:4} \end{equation}donde \(k_{1}=0.5\), \(k_{2}=5\) y el control está dado por
\begin{equation} \label{eq:6} u = a_{1} x_{1} + a_{2} x_{2} + 0.5 \sin(w t) \end{equation}con \(a_{1}=0.1\), \(a_{2}=0.2\) y \(w=100\).
El modelo, el control y las condición iniciales, pueden expresars en Python así:
def modelo(x,t): x1,x2=x k1,k2 = (0.5,5) x1p = -k1*(x1 - 1 + u(x,t) ) x2p = -k2*(x2 - 1.5 + u(x,t) ) xp = [x1p,x2p] return xp def u(x,t): x1,x2=x a1 = 0.1 a2 = 0.2 w = 100 control = a1*x1 + a2*x2 + 0.5*math.sin(w*t) return control x_0 = [0,0]
La función plot puede graficar una lista de secuencias, por lo que no es necesario cambiar en nada el código para graficar los resultados. El código completo para simular el sistema \eqref{eq:4} con el control \eqref{eq:6} resulta
import numpy as np import math from scipy.integrate import odeint import matplotlib.pyplot as plt # El modelo recibe un vector y devuelve un vector def modelo(x,t): x1,x2=x k1,k2 = (0.5,5) x1p = -k1*(x1 - 1 + u(x,t) ) x2p = -k2*(x2 - 1.5 + u(x,t) ) xp = [x1p,x2p] return xp # El control depende del estado y de t def u(x,t): x1,x2=x a1 = 0.1 a2 = 0.2 w = 100 control = a1*x1 + a2*x2 + 0.5*math.sin(w*t) return control # La condición inicial es un vector x_0 = [0,0] # Genera un arreglo de 101 puntos que van de 0 a 10 t_ini = 0 #t inicial t_fin = 10 #t final t_step = 0.01 #tamaño del paso de integración n_m = (t_fin - t_ini)/t_step +1 #numero de muestras t = np.linspace(t_ini,t_fin,n_m) # Realiza la simulación x = odeint(modelo,x_0,t) # Grafica los resultados plt.plot(t,x) plt.xlabel('t') plt.ylabel('x(t)') plt.show()
4. Simulación de sistemas dinámicos usando Octave
4.1. Introducción
Octave es un programa de software libre que tiene enfoque en realizar cálculos numéricos, de modo que es muy utilizado para resolver ecuaciones lineales y no lineales aunque sus aplicaciones abarcan también análisis estadísticos. La sintaxis del programa es muy similar a la de Matlab, es decir, trabaja a través de matrices y es posible compilar archivos creados en Matlab que tengan por ende la extensión .m. El presente trabajo muestra mediante algunos ejemplos la manera en la que se pueden simular los sistemas de primer y segundo orden, la simulación de un péndulo simple y como agregar un control a cualquier sistema.
4.2. Simulación de sistemas de primer orden
A diferencia de Python, no es necesario importar ninguna librería, se debe definir la ecuación de estados del sistema. Considere el sistema de primer orden expresado en su ecuación de estado como sigue:
\begin{equation} \dot{x}=ax+bu \end{equation}Para expresarlo en código, es necesario definir primero algo que se llama \(function handles\) que representa una función que apunta o toma de referencia a otra función y su sintaxis es la siguiente:
name = @function
Por ejemplo:
a = @sin
En donde a toma de referencia a la función seno. Esta propiedad permite pasar una función como argumento a otra función, algo que será útil para después, por el momento, podríamos definir el sistema (1) como:
xp = @[a*x+b*u];
Sin embargo, falta un detalle que corresponde a los argumentos de la función con los que sera evaluada, como sabemos hay una \(x\) para un instante de tiempo t, por lo tanto, la función debe trabajar con los argumentos x y t:
xp = @(t,x)[a*x+b*u];
Continuando con la parte que se encarga de resolver la ecuación diferencial, se tiene la función ode45 la cual recibe tres argumentos:
- El sistema, definido anteriormente como \(xp\).
- El intervalo de tiempo en el que se evaluará la ecuación el cual es un vector que contiene el tiempo inicial y el tiempo final.
- Las condiciones iniciales del sistema.
La solución es almacenada en un vector columna por cada estado en el instante de tiempo especificado. La sintaxis es la siguiente:
[t,y] = ode45(xp, [t\_start,t\_end],cond);
El intervalo de tiempo y la condición inicial son únicamente constantes, solo hay que definirlas:
t_start = 0; step = 0.1; t_end = 10; x_0 = 0;
Solo resta graficar los datos obtenidos, dado que \(y\) tiene la misma longitud que \(t\), se puede realizar una gráfica \(y\) vs \(t\) con el comando plot:
plot(t,y)
Finalmente el código completo para simular el sistema es:
#Sistema de primer orden #Constantes del sistema a = -1; b = 1; u = 1; #Intervalo de tiempo t_start = 0; t_end = 10; step = 0.1; #Condicion inicial x_0 = 0; #Sistema xp = @(t,x)[a*x + b*u]; #Solucion [t,y] = ode45(xp, [t_start:step:t_end], x_0); #Grafica plot(t,y)
| 9 | 14 | 19 | 24 | 29 | 34 | 39 | 44 | 49 | 54 |
4.3. Simulación de sistemas de segundo orden
La primer diferencia y muy clara esta, es que ahora se cuenta con dos estados, por lo que podría pensarse que habría que declarar dos funciones, sin embargo no es necesario, bueno de hecho no del todo, la función \(xp\) que se declaró anteriormente puede contener un arreglo de n-funciones a las cuales este apuntando, en este caso apuntará a cada función de cada estado, para darnos una idea:
xp = @(t,y)[xp1;xp2];
Es importante que cada función se encuentre separada por un punto y coma, de lo contrario el programa arrojará un mensaje de error.
Considere el sistema descrito por:
\begin{equation} \dot{x_1}=ax_1+bx_2+u \end{equation} \begin{equation} \dot{x_2}=x_1 \end{equation}Ahora x es un vector de dos elementos a los cuales se puede acceder mediante paréntesis. El sistema quedará definido por:
xp = @(t,x)[a*x(1)+b*x(2)+u;x(1)];
También habrá que crear un arreglo de dos elementos que contenga las condiciones iniciales respectivas:
x1\_0 = 0; x2\_0 = 0; cond = [x1\_0,x2\_0];
[t,y] = ode45(xp, [t\_start:step:t\_end],cond);
Como se dijo anteriormente, la solución se encuentra almacenada en un vector de columnas, por lo que para un sistema de segundo orden se tiene un arreglo de \(m\) filas dependiendo del numero de muestras y \(n\) columnas de acuerdo al número de estados. Para poder graficar cada uno, es necesario especificar todas las filas de una columna y hacer lo mismo para la otra de la siguiente forma:
y(:,1) y(:,2)
De este modo, la función \(plot\) quedaría como:
plot(t,y(:,1),t,y(:,2))
El código completo se presenta a continuación:
#Constantes del sistema a = -7; b = -140; u = 1; #Intervalo de tiempo t_start = 0; t_end = 3; step = 0.01; #Condicion inicial x1_0 = 0; x2_0 = 0; cond=[x1_0,x2_0]; #Sistema xp = @(t,x)[a*x(1)+b*x(2)+u;x(1)]; #Solucion [t,y] = ode45(xp, [t_start:step:t_end], cond); #Grafica plot(t,y(:,1),t,y(:,2))
El desarrollo de este código se puede aplicar a diversos sistemas, uno de ellos un poco más complejo es el del péndulo simple, que a su vez es un sistema no lineal, sin embargo eso no representa un problema ya que el código se ejecuta de la misma manera como se verá a continuación.
EL péndulo simple está descrito por las siguientes ecuaciones:
\begin{equation} \dot{x_1}=x_2 \end{equation} \begin{equation} \dot{x_2}=(\frac{1}{j})*(-m*g*l*sin(x_1)-b*x_2+u) \end{equation}Las constantes corresponden respectivamente a:
- j = inercia
- m = masa
- g = gravedad
- l = longitud
- b = fricción
El código para simular el péndulo simple queda de la siguiente manera
#Pendulo simple #Constantes del sistema g = 9.81; l = 0.4; b = 0.1; m = 0.5; j = m*l*l; u = 0; #Intervalo de tiempo t_start = 0; t_end = 10; step = 0.01; #Condicion inicial x1_0 = pi/2; x2_0 = 0; cond=[x1_0,x2_0]; #Sistema xp = @(t,x)[x(2);(1/j)*(-m*g*l*sin(x(1))-b*x(2)+u)]; #Solucion [t,y] = ode45(xp, [t_start:step:t_end], cond); #Grafica plot(t,y(:,1),t,y(:,2))
Note que la posición inicial es \(\frac{pi}{2}\); además, no tiene ninguna entrada o control. El comportamiento es el esperado, se mantiene oscilando por un tiempo hasta que permanece en reposo.
4.4. Simulación de sistemas con control
Añadir un control al sistema implica añadir una función, pero, como será argumento de la ecuación de estados, se debe crear otra function handle.
Considere el sistema
\begin{equation} \dot{x}=-ax+u \end{equation}con la ley de control dada por
\begin{equation} u=k_p*(ref-x) \end{equation}A partir de lo explicado anteriormente, se sabe que el control se puede definir como
u = @(x)[k_p*(ref-x)]
Depende únicamente de un argumento, el cual será el valor de x,mismo que hay que definir dentro de la ecuación del sistema ya que, si declaramos de la siguiente manera
xp = @(t,x)[-a*x+u]
El programa arrojará un error el cual indica que las operaciones con function handle no esta permitido ya que no es un escalar, por ello se debe establecer cual es el argumento con el que será evaluada la función, es decir, con \(x\), de modo que la implementación correcta es
xp = @(t,x)[-a*x+u(x)]
El código completo se muestra a continuación
#Sistema con control #Constantes del sistema a = 0.1; kp = 1; ref = 1; #Intervalo de tiempo t_start = 0; t_end = 10; step = 0.01; #Condicion inicial x1_0 = 0; #Control u = @(x)[kp*(ref-x)]; #Sistema xp = @(t,x)[-a*x+u(x)]; #Solucion [t,y] = ode45(xp, [t_start:step:t_end], x1_0); #Grafica plot(t,y)