Domingo Cortés, Diego Martínez

1. Introducción

Se describe aquí la construcción de una herramienta de software para simular sistemas dinámico de manera programable. El hecho de que el simulador sea programable quiere decir que se puede especificar de forma relativamente sencilla cientos o miles de simulaciones que se harán de forma automática, es decir sin la supervisión del usuario.

El software descrito aquí, está desarrollado en racket que es una extensión del lenguaje de programación Scheme.

El documento está pensado para servir a cualquiera que inicie en programación para que pueda observar como se hace un software extenso. Así mismo los estudiantes de ingeniería pueden observar como los programar puede ayudarles a resolver problemas por ellos mismos sin depender de que exista o no un software comercial para ello.

2. Objetivos

2.1. Especificar sistemas rápidamente

Para lograr que la especificación de sistemas sea rápida esta debe hacerse de manera parecida a su notación matemática estándar. Una de las desventajas de Simulink es que la especificación de un sistema si bien es sencilla tiende a ser bastante lenta.

2.2. Realizar una secuencia de simulaciones rápidamente

Suponga que se quieren simular decenas o cientos de controladores, el software debe tener instrucciones para hacer esto posible de una manera sencilla. Lo mismo para hacer simulaciones con una lista de parámetros o de condiciones iniciales. Esta será una de las características distintiva del simulador.

2.3. Interconectar sistemas

El simulador deberá tener instrucciones para interconectar sistemas. Por ejemplo dado dos sistemas dinámicos de deberán poder conectar en retroalimentación; en cascada o en suma.

3. Elementos del simulador

En la figura Sistema Típico se muestra el diagrama de un caso típico de simulación. El sistema consiste de

Una fuente para generar señales
Un restador de señales (comparador)
Un sistema dinámico
Un sistema estático (controlador)
Un osciloscopio para almacenar las señales que se generen durante la simulación.

Si la simulación se hiciera manualmente, la actualización del estado del sistema al pasar del tiempo \(t-1\) a \(t\) se haría como sigue:

Primero se calcularía el valor de la salida de la fuente en el tiempo \(t\).
Después se actualizaría la salida de los sistemas estáticos: el controlador y el comparador.
Con estos datos se actualizaría el estado del sistema dinámico utilizando un algoritmo de integración adecuado.
Actualizar la salida del sistema dinámico.
Finalmente se agregaría la nueva salida del sistema a los valores previos almacenados en el osciloscopio.

Esta secuencia de pasos es la misma que implementa en el simulador. Para ello es necesario un mecanismo que asegure la correcta secuencia de las acciones.

Cabe hacer notar que en la figura Sistema Típico se mencionan los elementos mínimos, sin embargo, en una simulación podría haber más de uno de los distintos bloques.

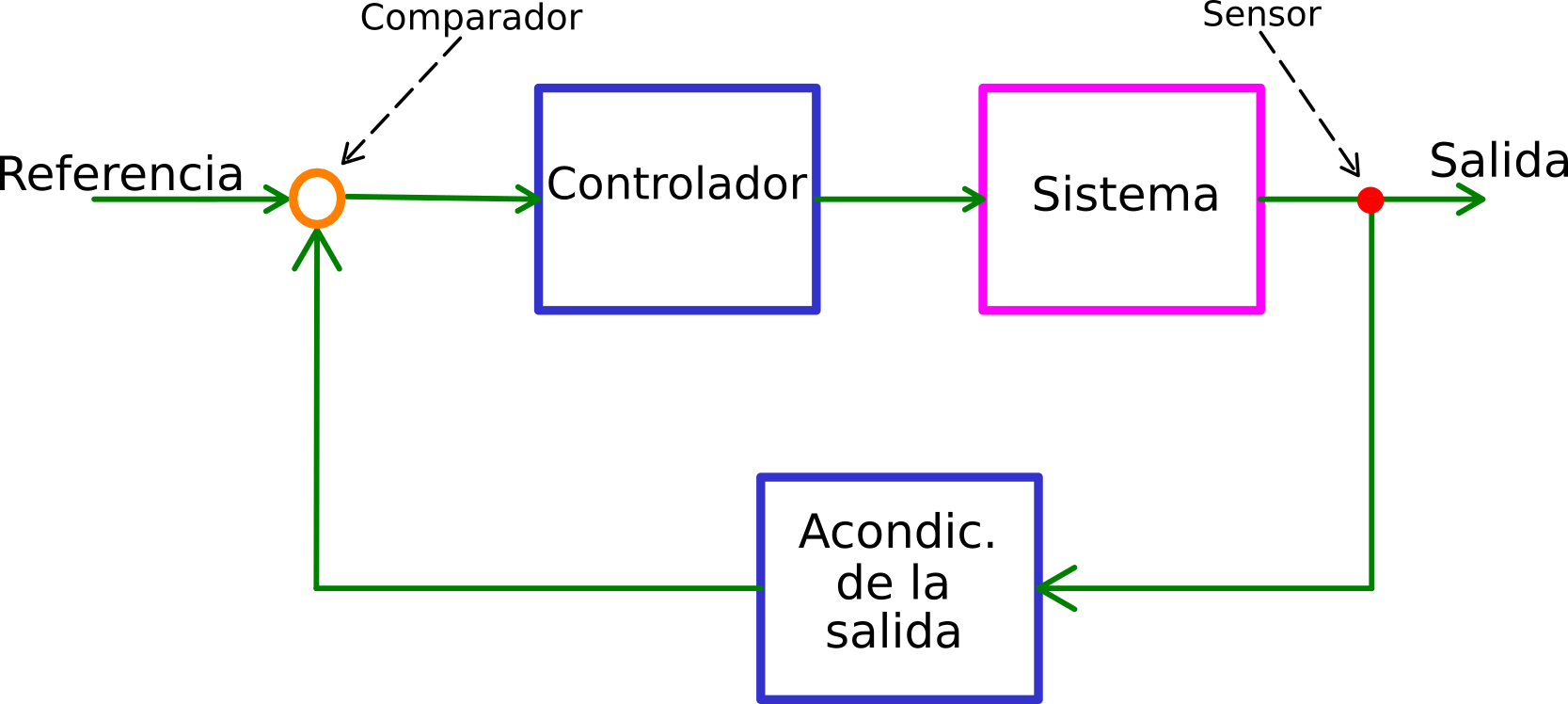
Figure 1: Un sistema de control típico

4. Modelo de simulación

El modelo de simulación que se plantea es que cada uno de los elementos que participan en una simulación están contenidos dentro de un bloque. La conexión de los bloques es independiente del comportamiento de cada bloque. De tal manera que se pueden especificar primero el comportamiento de cada bloque y después las conexiones o viceversa.

Como consecuencia el comportamiento de los bloques se puede modificar entre simulación y simulación. Esto permite realizar una secuencia de simulaciones variando el comportamiento de uno o más bloques de la simulación.

Los bloques tienen puertos (pto) de entrada y salida. La comunicación entre los bloques se hace a través de sus puertos mediante alambres (wires).

Un reloj (clock) mantiene todos los procedimientos que es necesario ejecutar cuando se inicia la simulación. Así mismo mantiene los procedimientos necesarios para avanzar del tiempo \(t-1\) al tiempo \(t\), además de los procedimientos que ser requieren al terminar una simulación. El reloj recibe mensajes de inicio de simulación, de avance de la simulación y de fin de simulación.

Cuando se crea un bloque, además del tipo de elemento que se trate, sólo es necesario especificar el número de entradas y salidas. En el caso de las fuentes tiene \(0\) entradas y los osciloscopios tienen \(0\) salidas. Al momento de crearse, cada bloque crea los alambres necesarios para su conexión. Además, se informa al clock los procedimientos necesarios para inicializarse; para actualizarse cada vez que avance el reloj y para finalizar la simulación.

La conexión de los bloques se hace mediante alambres wires. Un alambre es un objeto que mantiene el valor de una señal y recibe mensajes para cambiar o informar dicho valor. Para realizar una conexión es necesario crear un alambre y especificar un puerto de origen y un puerto de destino. Un puerto está formado por el nombre de un bloque y un número. El número indica de que alambre se trata. La conexión se realiza mediante mensajes a los bloques de origen y fin del alambre.

El comportamiento de los bloques de sistemas estáticos se especifica mediante una lista de expresiones simbólicas (s-expressions) que determinan las salidas del bloque en función de las entradas; estas expresiones pueden depender de parámetros. Los símbolos para especificar las entradas y los parámetros no son determinados de antemano, por lo que es necesario especificarlos. Además antes de una simulación es necesario especificar los valores de los parámetros.

Para especificar el comportamiento de los bloques de sistemas dinámicos es necesario lo mismo que para sistemas estáticos. Además en estos bloques son necesarias las expresiones simbólicas para la derivada de los estados y los símbolos paras los estados. Antes de iniciar una simulación deben especificarse las condiciones iniciales de los estados y los valores de los parámetros.

Los bloques de fuentes son como sistemas estáticos sin entradas. Las expresiones simbólicas que especifican su comportamiento dependen del símbolo t que se asocia al tiempo de simulación y de parámetros. Los símbolos de los parámetros no están predeterminados por lo que es necesario especificarlos. Antes de iniciar una simulación es necesario especificar el valor de los parámetros.

Los bloques de osciloscopio no tienen salidas ni expresiones que determinen su comportamiento. Cada vez que avanza el reloj almacena el valor de la señal de los alambres de entrada. Al terminar una simulación trasfiere todas las señales a un almacén de resultados de simulación. Esto es útil en el caso de una secuencia se simulaciones.

A partir de estos elementos generales se pueden construir elementos particulares. Por ejemplo, en el caso de las fuentes, se puede construir una fuente de senoidal, o escalón. A partir del elemento general estático se puede construir un sumador, un comparador, una ganancia, etc. A partir del bloque dinámico general se puede hacer un integrador, un primer orden, etc.

También se pueden realizar conexiones comunes. Por ejemplo se pueden conectar sistemas en cascada o en paralelo. Se puede también hacer una estructura de un sistema y después especificar el comportamiento de cada bloque.

Se pueden generar secuencia de valores para un bloque en particular y hacer una simulación para cada valor de los parámetros. O bien hacer una secuencia de bloques y hacer una conexión (y una simulación) para cada bloque.

5. Programación de los elementos de una simulación

En general un sistema para ser simulado consta de

Reloj
Fuentes
Bloques estáticos
Bloques dinámicos
osciloscopios
Alambres
Controlador de simulación

5.1. El reloj (clock)

El reloj clock conoce todos los procedimientos que se necesitan ejecutar al inicio de una simulación; los que se necesitan para avanzar el estado desde el tiempo \(t-1\) a \(t\); y los que se deben ejecutar al final de una simulación.

El clock mantiene varias listas de procedimientos que se deben ejecutar al inicio de una simulación. Estas listas son procedimientos de inicialización de:

fuentes init-src-procs
bloques estáticos init-static-procs
el estado de los sistemas dinámicos init-sys-state-procs
salidas de los sistemas dinámicos init-sys-out-procs
osciloscopios init-sink-procs

A cada cada paso de integración o tic del reloj se deben ejecutar una serie de procedimientos que el reloj mantiene para cada bloque. Estas listas mantienen los procedimientos para la actualización de:

fuentes src-procs
bloques estáticos static-procs
el estado de los bloques dinámicos sys-state-procs
la salida de los bloques dinámicos sys-out-procs
los valores almacenados en los osciloscopios sink-procs

Además el reloj mantiene una lista de procedimientos que se ejecutan al final de una simulación: end-procs.

Cuando se crea un bloque, éste informa al reloj el procedimiento de inicialización, el procedimiento para actualizarse al avanzar el reloj y el procedimiento se debe ejecutar (si acaso) al finalizar una simulación.

Para actualizar estas listas de acciones el clock recibe los siguientes mensajes:

add-init-src-proc!
add-init-static-proc!
add-init-sys-state-proc!
add-init-sys-out-proc!
add-init-sink-proc!
add-src-proc!
add-static-proc!
add-sys-state-proc!
add-sys-out-proc!
add-sink-proc!
add-end-proc!

Cada uno de esto mensajes recibe un proceso para agregarlo a la lista respectiva.

Durante una simulación el reloj (clock) mantiene el tiempo de simulación (sim-time) y el paso de integración (dt). Note que el reloj no mantiene el tiempo final.

Al iniciarse el simulación el reloj recibe el mensaje init-sim! que ejecuta todos los procedimientos de inicialización.

Después de iniciada una simulación, cada vez que el reloj recibe el mensaje tic! ejecuta todos los procedimientos necesarios para avanzar el estado del sistema del tiempo \(t-1\) al tiempo \(t\)

El reloj también recibe el mensaje end-sim! que causa que se ejecuten todos los procedimientos necesarios para terminar una simulación.

Cuando recibe los mensajes get-time y get-dt, el reloj informa el tiempo de simulación y el paso de integración respectivamente.

Hay un objeto que controla la simulación (sim). Este objeto se encarga de madar los mensajes init-sim!, tic! y end-sim! al reloj. El funcionamiento de este objeto se explica más adelante.

El procedimiento (make-clock) crea un objeto con todas las características descritas. Tal como está el simulador sólo es necesario un reloj por lo que se define el objeto sim-clock que es conocido en todo el programa.

El archivo clock.rkt contiene el código del reloj y se muestra a continuación.

#lang racket

(require "../fnc/auxfnc.rkt")   ; general support functions

;; ==========  general clock ==========  
(define (make-clock)
  (let ([sim-time null]          ; simulation time 
        [dt null]                ; integration step size
        ;; list of initialization procedures
        [init-src-procs null]     
        [init-static-procs null]
        [init-sys-state-procs null] 
        [init-sys-out-procs null]  
        [init-sink-procs null]  
        ;; list of tic! procedures
        [src-procs null]        ; update sources values
        [static-procs null]     ; update static systems
        [sys-state-procs null]      ; update state of dynsys 
        [sys-out-procs null] ; update output of dynsys
        [sink-procs null]       ; update sinks (scopes) 
        ;; procedures run at end
        [end-procs null])       ; to end the simulation
         
    (define (add-init-src-proc! proc)
      (set! init-src-procs (cons proc init-src-procs)))

    (define (add-init-static-proc! proc)
      (set! init-static-procs (cons proc init-static-procs)))

    (define (add-init-sys-state-proc! proc)
      (set! init-sys-state-procs
            (cons proc init-sys-state-procs)))

    (define (add-init-sys-out-proc! proc)
      (set! init-sys-out-procs
            (cons proc init-sys-out-procs)))

    (define (add-init-sink-proc! proc)
      (set! init-sink-procs (cons proc init-sink-procs)))

    (define (add-src-proc! proc)
      (set! src-procs (cons proc src-procs)))

    (define (add-static-proc! proc)
      (set! static-procs (cons proc static-procs)))

    (define (add-sys-state-proc! proc)
      (set! sys-state-procs (cons proc sys-state-procs)))

    (define (add-sys-out-proc! proc)
      (set!  sys-out-procs (cons proc sys-out-procs)))

    (define (add-sink-proc! proc)
      (set! sink-procs (cons proc sink-procs)))

    (define (add-end-proc! proc)
      (set! end-procs (cons proc end-procs)))

    (define (init-sim! sim-t0 sim-dt)
      (set! sim-time sim-t0)
      (set! dt sim-dt)
      (call-each init-src-procs)
      (call-until-no-more-changes init-static-procs)
      (call-each init-sys-state-procs)
      (call-each init-sys-out-procs)
      (call-each init-sink-procs))

    (define (tic!)
      (set! sim-time (+ sim-time dt))
      (call-each src-procs)
      (call-until-no-more-changes static-procs)
      (call-each sys-state-procs)
      (call-each sys-out-procs)
      (call-each sink-procs))

    (define (end-sim!)
      (call-each end-procs))

    (lambda (msg . args)
      (case msg
        [(get-time) sim-time]
        [(get-dt) dt]

        [(init-sim!)            (apply init-sim! args) ]
        [(tic!)                 (apply tic! args)]
        [(end-sim!)             (apply end-sim! args)]
        
        [(add-init-src-proc!)   (apply add-init-src-proc! args)]
        [(add-init-static-proc!) (apply add-init-static-proc! args)]

        [(add-init-sys-state-proc!)
         (apply add-init-sys-state-proc! args)]
        
        [(add-init-sys-out-proc!)
         (apply add-init-sys-out-proc! args)]

        [(add-init-sink-proc!)  (apply add-init-sink-proc! args)]
        [(add-src-proc!)        (apply add-src-proc! args)]
        [(add-static-proc!)     (apply add-static-proc! args)]
        [(add-sys-state-proc!)      (apply add-sys-state-proc! args)]
        [(add-sys-out-proc!) (apply add-sys-out-proc! args)]
        [(add-sink-proc!)       (apply add-sink-proc! args)]
        [(add-end-proc!)        (apply add-end-proc! args)]
        [else (error "Unknown operation on CLOCK" msg)]))))


;; ==========  simulation clock ==========  
(define sim-clock (make-clock))

;; export all defined function
(provide (all-defined-out))

5.2. Bloques de sistemas estáticos

Para crear un sistema estático (static-sys) sólo es necesario especificar el número de entradas y salidas denotadas por n-in y n-out respectivamente. El procedimiento para crear un sistema estático es

(define nombre-del-sistema (make-static-sys num-ent num-sal))

donde nombre-del-sistema es el nombre con que se identificará el bloque a partir de su creación; num-ent es el número de entradas y num-sal es el número de salidas.

El comportamiento de un sistema estático se especifíca con una lista de expresiones simbólicas (s-expression). En la s-expression pueden haber símbolos que denotan entradas y símbolos que denotan parámetros. Por ello es necesario especificar los símbolos para las entradas y los símbolos para los parámetros. Además antes de iniciar una simulación deben especificarse los valores de los parámetros. El siguiente código determina el comportamiento de un sistema estático de dos entradas y dos salidas. La primera salida del sistema está determinada por \(au_{1} + bu_{2}\) y la segunda por \(au_{1} - bu_{2}\) donde \(u_{1}\) y \(u_{2}\) son entradas y \(a\) y \(b\) son parámetros. De correrse una simulación con este código los valores de \(a,b,c,d\) serían \(1,1,2,2\).

(define block2x2 (make-static-sys 2 2))
(block 'set-in-symb! '(u1 u2))
(block 'set-prmtr-symb! '(a b c d))
(block 'set-out-expr! '(
                        (+ (* a u1) (* b u2))
                        (- (* c u1) (* d u2))))
(block 'set-prmtr-val! (list 1 1 2 2))

Cuando se crea un sistema estático se crean n-in alambres de entrada y n-out alambres de salida. Inicialmente estos alambres son del tipo null-wire que después serán substituidos por alambres que provengan o vayan a otros bloques. Un null-wire es un alambre cuya señal siempre es cero.

Además de los alambres, un bloque estático mantiene una lista de símbolos (in-symb) que denotan las entradas; una lista de parámetros (prmtr-symb) que denotan los parámetros; una lista de expresiones simbólicas que determinan el valor de las salidas. Estas expresiones dependen de las entradas y los parámetros. Un bloque estático guarda el valor previo de las salidas (prev-in-signals). Al guardar el valor previo de las salidas se puede determinar si se necesita actualizar las salidas o no. Todas las variables mencionadas en este párrafo tienen el valor de null al inicio y son modificadas después.

Cada bloque de sistema estático admite los mensajes:

n-in informa el número de entradas
n-out informa el número de salidas
in-wires expone a los demás bloques los alambres de entrada, esto es útil para crear conexiones predeterminadas.
out-wires expone a los demás bloques los alambres de salida
in-symb Informa cual es la lista de símbolos para denotar las entradas.
prmtr-symb Informa cual es la lista de símbolos para denotar los parámetros.
out-expr Informa cuales son las expresiones simbólicas para determinar las salidas a partir de las entradas y los parámetros.
prmtr-val Informa el valor de los parámetros.
set-in-connexion! Sustituye uno de los alambres de entrada que inicialmente es un null-wire por un alambre útil. Para ello es necesario que reciba un alambre y el número de entrada de que se trata.
set-out-connexion! Igual que el mensaje anterior pero para un alambre de salida.
set-in-symb! Establece los símbolos para denotar las entradas.
set-prmtr-symb! Establece los símbolos para denotar los parámetros.
set-out-expr! Establece las expresiones simbólicas para determinar las salidas.
set-prmtr-val! Establece los valores de los parámetros.

Cuando se crea un sistema estático se agrega el procedimiento update-output-if-necessary! a las listas init-static-proc y static-proc que mantiene el reloj. Esto se hace mandando los mensajes adecuados al reloj.

El procedimiento update-output-if-necessary! actualiza las salidas del bloque sólo cuando ha cambiado la señal de entrada. Para ello es necesario que el bloque mantenga la entrada previa prev-in-signal. Cuando el bloque no es necesario actualizar la salida el procedimiento devuelve #f y cuando sí fue necesario devuelve #t. Los procedimientos update-output-using! y update-output-signals! son procedimientos auxiliares en la actualización de la salida. El procedimiento update-output-using! evalúa las expresiones de salida usando las señales de entrada actuales. El procedimiento update-output-signals! recibe los valores que han de ponerse en los alambres de salida y manda un mensaje a cada alambre de salida para que actualice sus valores.

A continuación se presenta el código que genera los bloques estáticos

#lang racket

(require "../fnc/auxfnc.rkt")   ; general support functions
(require "clock.rkt")
(require "sim.rkt")
(require "wires.rkt")

;; ========== General static block ==========  
(define (make-static-sys n-in n-out)
  (let ([in-wires   (map0 make-null-wire n-in)]
        [out-wires  (map0 make-null-wire n-out)]

        [in-symb     null]
        [prmtr-symb  null]
        [out-expr    null]
        [prmtr-val   null]

        [prev-in-signals null])

    (define (set-in-connexion! wire x)
      (set! in-wires (list-set in-wires x wire)))

    (define (set-out-connexion! wire x)
      (set!  out-wires (list-set out-wires x wire)))

    (define (set-out-expr! new-out-expr)
          (set! out-expr new-out-expr))

    (define (set-in-symb! new-in-symb)
          (set! in-symb new-in-symb))

    (define (set-prmtr-symb! new-prmtr-symb)
      (set! prmtr-symb new-prmtr-symb))

    (define (set-prmtr-val! new-prmtr-val) 
      (set! prmtr-val new-prmtr-val))

    (define (get-in-signals)
      ;; (displayln "getting static in-signal")
      (map (lambda (wire) (wire 'get-signal)) in-wires))

    (define (update-out-signals! vals)
      (for-each (lambda (out-wire val) (out-wire 'set-signal! val))
           out-wires vals))

    (define (update-output-using! current-in-signals)
      (let ([out-env
             (make-env (append in-symb prmtr-symb)
                       (append current-in-signals prmtr-val))])
        (update-out-signals! (eval-sexpr out-expr out-env))))
    
    (define (update-output-if-necessary!)
      ;; (displayln "updating static signal")
      (let ([current-in-signals (get-in-signals)])
        (if (equal? current-in-signals prev-in-signals)
            #f
            (begin
              (update-output-using! current-in-signals)
              (set! prev-in-signals (get-in-signals))
              #t))))

    ;; function to check detectable errors (to be programmed)
    (define (check-errors)
      null)

    (sim-clock 'add-init-static-proc!  update-output-if-necessary!)
    (sim-clock 'add-static-proc! update-output-if-necessary!)

    (lambda (msg . args)
      ;; connexion related msg
      (case msg
        [(n-in)                n-in]
        [(n-out)               n-out]
        [(in-wires)            in-wires]
        [(out-wires)           out-wires]
        [(set-in-connexion!)   (apply set-in-connexion! args)]
        [(set-out-connexion!)  (apply set-out-connexion! args)]

        ;; info getters
        [(in-symb)     in-symb]
        [(prmtr-symb)  prmtr-symb]
        [(out-expr)    out-expr]
        [(prmtr-val)   prmtr-val]
        
        ;; state setters
        [(set-in-symb!)     (apply set-in-symb! args)]
        [(set-prmtr-symb!)  (apply set-prmtr-symb! args)]
        [(set-out-expr!)    (apply set-out-expr! args)]    
        [(set-prmtr-val!)   (apply set-prmtr-val! args)]

        ;; debuggin msg
        [(uoin) (update-output-if-necessary!)]
        [(gs) (get-in-signals)]
        [else (error "Unknown operation on STATIC-SYS " msg)]))))

;; export all defined function
(provide (all-defined-out))

Una vez teniendo el código que bloques estáticos es sencillo generar bloques estáticos particulares. El siguiente código, genera

Una ganancia.
Un restador de dos señales, muy común en control.
Un sumador de dos o más señales.
Un distribuidor que acepta una señal y proporciona muchas salidas con la misma señal.
Un multiplicador.
Un bloque de una entrada y una salida que realiza cualquier función.

#lang racket

(require "../fnc/auxfnc.rkt")   ; general support functions
(require "static.rkt")

;; ========== Particular static blocks ==========  
;; gain block
(define (make-gain kp)
  (let ([gain (make-static-sys 1 1)])
    (gain 'set-in-symb!     '(u))
    (gain 'set-prmtr-symb!  '(k))
    (gain 'set-out-expr!    '((* k u)))
    (gain 'set-prmtr-val!   (list kp))
    gain))

;; error block: substract two signals
(define (make-diff)
  (let ([sub (make-static-sys 2 1)])
    (sub 'set-in-symb!     '(u1 u2))
    (sub 'set-prmtr-symb!  '())
    (sub 'set-out-expr!    '((- u1 u2)))
    sub))

;; y =  u_1 + u_2 + ... + u_n ; n = 2 by dflt
(define (make-adder [n 2])
  (let ([add (make-static-sys n 1)]
        [ent (make-list-of-symb "u" n)])
    (add 'set-in-symb!     ent)
    (add 'set-prmtr-symb!  '())
    (add 'set-out-expr!    (list (cons '+ ent)))
    add))

;; y_1 = y_2 = ... = y_n = u ; n = 2 by dflt
(define (make-distributor [n 2])
  (let ([dist (make-static-sys 1 n)])
    (dist 'set-in-symb!     '(u))
    (dist 'set-prmtr-symb!  '())
    (dist 'set-out-expr!    (map (lambda (x) (list 'u)) (range n)))
    dist))

;; y =  u_1 * u_2 * ... * u_n ; n = 2 by dflt
(define (make-mult [n 2])
  (let ([mult (make-static-sys n 1)]
        [ent (make-list-of-symb "u" n)])
    (mult 'set-in-symb!     ent)
    (mult 'set-prmtr-symb!  '())
    (mult 'set-out-expr!    (list (cons '* ent)))
    mult))

;; y = fn(u)
(define (make-func fn)
  (let ([func (make-static-sys 1 1)])
    (func 'set-in-symb!     '(u))
    (func 'set-prmtr-symb!  '(f))
    (func 'set-out-expr!    '((f u)))
    (func 'set-prmtr-val!   (list fn))
    func))

;; export all defined function
(provide (all-defined-out))

5.3. Bloques de sistemas dinámicos

El procedimiento make-dynsys crea un sistema dinámico. Para ello es necesario pasarle el número de entradas y salidas. El procedimiento típico para crear un sistema dinámico es

(define nombre-del-sistema (make-dynsys num-ent num-sal))

donde nombre-del-sistema es el nombre con que se identificará el bloque a partir de su creación; num-ent es el número de entradas y num-sal es el número de salidas.

Un sistema dinámico contiene todos los elementos y características de un sistema estático. Además un sistema dinámico debe mantener las expresiones para las derivadas de los estados (state-expr). Como consecuencia tambien es necesario especificar los símbolos que denotan los estados (state-symb) y antes de una simulación son necesarias las condiciones iniciales (init-cond).

La integración de los estados de un sistema dinámico se hace usando una biblioteca para solución de ecuaciones diferenciales. Esta biblioteca requiere saber:

La dimensión del sistema (dim) que se inicializa en \(0\)
El tiempo de simulación (t) y el paso de integración que se obtienen del reloj (sim-clock).
Una función que se aplica cada paso de integración (step). Al inicio esta función es null.
Una función que a partir de los estados devuelva su derivada (sim-sys). Al inicio esta función es null.
Un vector donde el algoritmo de integración almacena una estimación del error de integración (state-error). Al inicio este vector es null.
Un vector donde el algoritmo de integración recibe una estimación de la derivada del estado (state-deriv-in). Al inicio este vector es null.
Un vector donde el algoritmo de integración almacena una estimación de la derivada del estado después del cálculo de un nuevo estado (state-deriv-out). Al inicio este vector es null.

Además de los mensajes que recibe un sistema estático, cada bloque de sistema dinámico admite los mensajes:

dim informa la dimensión del sistema.
state-symb informa los símbolos que denotan los estados
state-expr informa las expresiones que determinan la derivada del estado.
state-val informa el valor del vector de estado.
init-cond informa el valor de las condición inicial del estado.
set-state-expr! Establece las expresiones para el cálculo de la derivada del estado.
set-state-symb! Establece los símbolos que denotan los elementos del vector de estado.
set-init-cond! Establece el valor de las condición inicial.

Cuando se crea un bloque dinámico se agregan los siguientes procedimientos al reloj:

init-sys! se agrega a la lista init-sys-state-proc!
update-output! se agrega a la lista init-sys-out-proc!
update-state! se agrega a la lista sys-state-proc!
update-output! se agrega a la lista sys-out-proc!

El procedimiento init-sys! revisa algunos errores en las expresiones que determinan el comportamiento del sistema (check-errors); determina la dimensión (dim) del sistema; crea los vectores (state-deriv-in, state-deriv-out, state-error) y las funciones necesarias (make-sim-aux) para el algoritmo de integración; hace que el vector de estado (state-val) sea igual a la condicion inicial (init-cond) y ejecuta un procedimiento (ode-system-function-eval) que calcula la derivada del estado al iniciar la simulación.

El procedimiento update-state! se corre en cada tic del reloj. Este procedimiento hace uso de la biblioteca para resolver ecuaciones diferenciales. Las funciones que está biblioteca requiere se crean automáticamente a partir de las expresiones de la derivada del estado (state-expr) al inicio de la simulación. Después de cada paso de integración la biblioteca devuelve un estimado de la derivada del estado (state-deriv-out).

El procedimiento update-output! evalua las expresiones que determinan la salida del sistema y actualiza la señal de los alambres de salida. Este procedimiento se corre al iniciar la simulación y en cada tic del reloj.

A continuación se muestra el código del procedimiento make-dynsys.

#lang racket
(require (planet williams/science/ode-initval)) ; integration library

(require "../fnc/auxfnc.rkt")   ; general support functions
(require "clock.rkt")
(require "sim.rkt")
(require "wires.rkt")

(define  (make-dynsys n-in n-out)
  (let (
        [in-wires   (map0 make-null-wire n-in)]
        [out-wires  (map0 make-null-wire n-out)]

        [xmax (sim-prmtr 'max-state-val)]
        [xmin (sim-prmtr 'min-state-val)]
        
        [t (lambda ()   (sim-clock 'get-time))]
        [dt (lambda ()  (sim-clock 'get-dt))]
        [dim            0]
        
        [state-expr  null]
        [out-expr    null]
        
        [state-symb  null]
        [in-symb     null]
        [prmtr-symb  null]
        
        [prmtr-val  null]          
        [init-cond  null]         
        
        [state-val  null]        
        
        ;; local values neccesary for integration algorithms
        [step             null]
        [sim-sys          null]
        [state-error      null] ; absolute error after integration step   
        [state-deriv-in   null] ; estimated deriv previous integration
        [state-deriv-out  null]); estimated deriv after integration

    (define (limit-val! x)  ;; limit a num x to be in [xmin, xmax]
      (if (> x xmax) xmax
          (if (< x xmin) xmin x)))

    (define (set-state-expr! new-state-expr)
      (set! state-expr new-state-expr))

    (define (set-out-expr! new-out-expr)
      (set! out-expr new-out-expr))
    
    (define (set-state-symb! new-state-symb)
      (set! state-symb new-state-symb))

    (define (set-in-symb! new-in-symb)
      (set! in-symb new-in-symb))
    
    (define (set-prmtr-symb! new-prmtr-symb)
      (set! prmtr-symb new-prmtr-symb))
    
    (define (set-prmtr-val! new-prmtr-val) 
      (set! prmtr-val new-prmtr-val))
    
    (define (set-init-cond! new-ic)  
      (set! init-cond new-ic))
    
    (define (set-in-connexion! wire x)
      (set! in-wires (list-set in-wires x wire)))
    
    (define (set-out-connexion! wire x)
      (set!  out-wires (list-set out-wires x wire)))
    
    (define (get-in-signals)
      (map (lambda (wire) (wire 'get-signal)) in-wires))
    
    (define (update-out-signals! vals)
      (for-each (lambda (out-wire val) (out-wire 'set-signal! val))
                out-wires vals))
    
    ;; function to check detectable errors (to be completed)
    (define (check-errors)
      (cond
        [(not (= (length state-expr) (length state-symb)))
         (displayln "state-expr and state-symb do not match")]
        [(not (= (length state-symb) (length init-cond)))
         (displayln "state-symb and init-cond do not match")]
        ))
    
    (define (init-sys!) ; procedures when the clock start
      (check-errors)
      (set! dim (length state-symb))
      (set! state-deriv-in (make-vector dim 0.0))
      (set! state-deriv-out (make-vector dim 0.0))
      (set! state-error (make-vector dim 0.0))
      (set! state-val (list->vector init-cond))
      (make-sim-aux-func!)
      (ode-step-reset step)
      (ode-system-function-eval sim-sys (t) state-val state-deriv-in)
      )
    
    (define (update-state!)
      (new-state)
      (vector-copy! state-deriv-in 0 state-deriv-out))
    
    (define (update-output!)
      (let ([out-env (make-env (append state-symb prmtr-symb in-symb)
                               (append (vector->list state-val)
                                       prmtr-val
                                       (get-in-signals)))])
        (update-out-signals! (eval-sexpr out-expr out-env))))
    
    ;; =========== begin integration procedures ===================
    ;; Procedures "step", "sim-func",  "sim-sys"
    ;; and "new-state" perform the integration
    (define (sim-func t state-val state-deriv params)
      (let ([sys-env
             (make-env (append state-symb prmtr-symb in-symb)
                       (append (vector->list state-val)
                               prmtr-val
                               (get-in-signals)))])
        (vector-copy! state-deriv 0
                      (list->vector (eval-sexpr state-expr sys-env)))))
    
    (define (make-sim-aux-func!)
      (set! sim-sys (make-ode-system sim-func #f dim null))
      (set! step                  ; create an step function
            (make-ode-step (sim-prmtr 'int-method) dim)))
    
    (define (new-state)                   ; get the new state values
      ;; (displayln "before updating the state: ")
      ;; (display-sim-data)
      (ode-step-apply
       step
       (t)
       (dt)
       state-val
       state-error
       state-deriv-in
       state-deriv-out
       sim-sys)
      (vector-map! limit-val! state-val)
      )
    ;; ============ end integrations functions ==========
    
    ;; add procedures to sim-clock
    (sim-clock 'add-init-sys-state-proc!  init-sys!)
    (sim-clock 'add-init-sys-out-proc!    update-output!)
    (sim-clock 'add-sys-state-proc!       update-state!)
    (sim-clock 'add-sys-out-proc!         update-output!)
    
    ;; function for debuggin
    (define (display-sim-data)
      (displayln "Sim-data: ") 
      (dp2 "t: "                  (t))
      (dp2 "dt: "                 (dt))
      (dp2 "state-val: "          state-val)
      (dp2 "state-error:  "       state-error) 
      (dp2 "state-deriv-in:  "    state-deriv-in) 
      (dp2 "state-deriv-out:  "   state-deriv-out)
      (dp2 "int-method:  "        (ode-step-name step) )
      (dp2 "int-method order:  "  (ode-step-order step))
      (nl)
      ) 
    
    (lambda (msg . args)
      (case msg
        ;; connexion related msg
        [(n-in)                n-in]
        [(n-out)               n-out]
        [(in-wires)            in-wires]
        [(out-wires)           out-wires]
        [(set-in-connexion!)   (apply set-in-connexion! args)]
        [(set-out-connexion!)  (apply set-out-connexion! args)]
        
        ;; info getters
        [(dim)         dim]
        [(state-symb)  state-symb]
        [(in-symb)     in-symb]
        [(prmtr-symb)  prmtr-symb]
        [(state-expr)  state-expr]
        [(out-expr)    out-expr]
        
        ;; state getters
        [(state-val)  state-val]
        [(prmtr-val)  prmtr-val]
        [(init-cond)  init-cond]
        
        ;; state setters
        [(set-state-expr!)  (apply set-state-expr! args)]
        [(set-out-expr!)    (apply set-out-expr! args)]       
        [(set-state-symb!)  (apply set-state-symb! args)]
        [(set-prmtr-symb!)  (apply set-prmtr-symb! args)]
        [(set-in-symb!)     (apply set-in-symb! args)]        
        [(set-init-cond!)   (apply set-init-cond! args) ]
        [(set-prmtr-val!)   (apply set-prmtr-val!  args)]
        
        ;; debuggin msg
        [(gs)              (get-in-signals)]
        [(init-sys!)       (apply init-sys! args)]
        [(update-state!)   (apply update-state! args)]
        [(update-output!)  (apply update-output! args)]
        [(sim-data)        (display-sim-data)]

        [else (error "Unkow operation DYNSYS" msg)]))
    ))

;; export all defined function
(provide (all-defined-out))

5.4. Bloques de fuentes

El procedimiento make-src crea un bloque del tipo fuente. Para ello es necesario pasarle el número de salidas. El procedimiento tipico para crear una fuente es:

(define nombre-dela-fuente (make-src num-sal))

Los bloques de fuentes son como los sistemas estáticos pero no tienen alambres de entrada. Así, no incluyen todos los datos y procedimientos de los sistemas estáticos que se refieren a las entradas.

Por ejemplo, en los bloques de fuentes las expresiones de salida no incluyen símbolos que denoten entradas. Dichas expresiones sólo dependen de símbolos que denotan parámetros y del símbolo t que denota el tiempo de simulación. El valor de este símbolo se obtiene del reloj.

Cada bloque de fuente admite los siguientes mensajes

n-in informa el número de entradas que siempre es cero. Aunque los bloques de fuentes no tienen entradas, es conveniente que puedan informar a los demás bloques que tienen \(0\) entradas.
n-out informa el número de salidas
out-wires expone a los demás bloques los alambres de salida.
prmtr-symb Informa cual es la lista de símbolos para denotar los parámetros.
out-expr Informa cuales son las expresiones simbólicas para determinar las salidas a partir del tiempo (t) los parámetros.
prmtr-val Informa el valor de los parámetros.
set-out-connexion! Sustituye uno de los alambres de salida que inicialmente es un null-wire por un alambre útil. Para ello es necesario que reciba un alambre y el número de entrada de que se trata.
set-prmtr-symb! Establece los símbolos para denotar los parámetros.
set-out-expr! Establece las expresiones simbólicas para determinar las salidas.
set-prmtr-val! Establece los valores de los parámetros.

Cada que se crea un bloque de fuente se agrega el procedimiento update-output! a las listas init-src-proc y src-proc que mantiene el reloj. Este procedimiento actualiza las salidas de la fuente. Así al iniciar la simulación y en cada tic del reloj, la fuente actualiza su salida.

A continuación se muestra el código del procedimiento make-src El código también incluye la realización de fuentes comunes como función escalón, rampa, senoide y PWM.

#lang racket

(require "../fnc/auxfnc.rkt")   ; general support functions
(require "clock.rkt")
(require "wires.rkt")

;; ==========  Sources ==========
(define (make-src [n-out 1])
  (let ([n-in        0]
        [out-wires   (map0 make-null-wire n-out)]
        [prmtr-symb  null]
        [out-expr    null]
        [prmtr-val   null])

    (define (set-out-connexion! wire x)
      (set!  out-wires (list-set out-wires x wire)))

    (define (set-out-expr! new-out-expr)
          (set! out-expr new-out-expr))

    (define (set-prmtr-symb! new-prmtr-symb)
      (set! prmtr-symb new-prmtr-symb))

    (define (set-prmtr-val! new-prmtr-val) 
      (set! prmtr-val new-prmtr-val))

    (define (update-out-signals! vals)
      (for-each (lambda (out-wire val) (out-wire 'set-signal! val))
                out-wires vals))

    (define (update-output!)
      (let ([out-env
             (make-env (cons 't prmtr-symb)
                       (cons (sim-clock 'get-time) prmtr-val))])
        (update-out-signals! (eval-sexpr out-expr out-env))))

    (define (check-errors)
      (cond
        [(not (= (length out-expr) n-out))
         (displayln "Expressions and output numbers do not match")]))

    (define (check-errors-and-update-output!)
      (check-errors)
      (update-output!))

    (sim-clock 'add-init-src-proc! check-errors-and-update-output!)
    (sim-clock 'add-src-proc!  update-output!)

    ;; debugging msg
    (define (output-signals)
      (map (lambda (wire) (wire 'get-signal)) out-wires))
    
    (lambda (msg . args)
      (case msg
        [(n-in)                n-in]
        [(n-out)               n-out]
        [(set-out-connexion!)  (apply set-out-connexion! args)]

        [(set-prmtr-symb!)  (apply set-prmtr-symb! args)]
        [(set-out-expr!)    (apply set-out-expr! args)]
        [(set-prmtr-val!)   (apply set-prmtr-val! args)]

        [else (error "Unknown operation on SOURCE " msg)]))))

;; ========== Particular Sources ==========  
(define (make-step-src [val 1.0])
  (let ([step-src (make-src)])
    (step-src 'set-prmtr-symb! '(k))
    (step-src 'set-out-expr!   '((k)))
    (step-src 'set-prmtr-val!  (list val)) 
    step-src))

(define (make-impulse-src [val 1.0] [timeh .01])
  (let ([impulse-src (make-src)])
    (impulse-src 'set-prmtr-symb! '(k tu))
    (impulse-src 'set-out-expr!   '((if (< t tu) k 0.0)))
    (impulse-src 'set-prmtr-val!  (list val timeh)) 
    impulse-src))

(define (make-sin-src  [amp 1.0] [freq 1.0] [phase 0.0])
  (let ([sin-src (make-src)])
    (sin-src 'set-prmtr-symb! '(a w theta))
    (sin-src 'set-out-expr!   '((* a (sin (+ (* w  t) theta)))) )
    (sin-src 'set-prmtr-val!  (list amp freq phase))
    sin-src))

(define (make-ramp-src  [spd 1.0])
  (let ([ramp-src (make-src)])
    (ramp-src 'set-prmtr-symb!  '(s))
    (ramp-src 'set-out-expr!    '((* s t)))
    (ramp-src 'set-prmtr-val!   (list spd))
    ramp-src))

(define (make-pwm-src  [amp 1.0] [hit .5] [lot .5] [offset 0.0])
  (let ([pwm-src (make-src)]
        [freq (+ hit lot)])
    (pwm-src 'set-prmtr-symb!  '(a f h ost))
    (pwm-src 'set-out-expr! '((if (>
                                   (- (/ t f) (truncate (/ t f)))
                                   (/ h f))
                                  (- ost a)
                                  (+ ost a))))
    (pwm-src 'set-prmtr-val!   (list amp freq hit offset))
    pwm-src))

;; export all defined function
(provide (all-defined-out))

5.5. Bloques de osciloscopio

Un bloque de osciloscopio se crea con el procedimiento make-scope. Dicho procedimiento recibe un número que especifica el número de entradas, siendo 1 por defecto. La instrucción típida para crear un bloque de osciloscopio es:

(define nombre-del-osciloscopio (make-scope num-sal))

A diferencia del resto de los bloques el osciloscopio no tiene expresiones que definan su comportamiento. El objetivo de este bloque es almacenar las señales de los alambres de entrada durante una simulación.

Durante una simulación los datos del osciloscopio (data) se almacenan en un vector que puede crecer (grovable vector: gvector). Si estos datos se mandan al exterior se convierten a un vector normal mediante el procedimiento gvector->vector.

Los mensajes que admite un bloque de osciloscopio son

n-in que informa el número de entradas
n-out que devuelve siempre cero. Aunque los bloques de osciloscopio no tienen salidas, es conveniente que puedan informar a los demás bloques que tienen \(0\) entradas.
data devuelve un vector de los datos almacenados en el osciloscopio.
in-wires expone a los demás bloques los alambres de entrada, esto es útil para crear conexiones predeterminadas.
set-in-connexion! tiene la misma función que en el resto de los bloques.

Cuando un bloque de osciloscopio es creado se agrega el procedimiento init-scope a la lista init-sink-proc; add-newdata a la lista sink-proc y add-data-to-results a la lista end-proc.

El procedimiento init-scope limpia los datos almacenados en el osciloscopio (por si hubiera una simulación previa) y captura el valor de la señal de los alambres de entrada en el tiempo \(t0\). El procedimiento add-newdata agrega los datos de entrada a los datos almacenados en el osciloscopio. Este procedimiento se ejecuta en cada tic del reloj. El procedimiento add-data-to-results transfiere los datos almacenados en el osciloscopio a un "almacén" de resultados de simulación. Este procedimiento se ejecuta al término de una simulación.

A continuación se muestra el código necesario para implementar osciloscopios

#lang racket
(require data/gvector)  ; scope uses growable vectors

(require "../fnc/auxfnc.rkt")   ; general support functions
(require "clock.rkt")
(require "sim.rkt")
(require "wires.rkt")

;; ===== sinks =====
(define (make-scope [n-in 1])
  (let ([data      (make-gvector)]
        [in-wires  (map0 make-null-wire n-in)])

    (define (set-in-connexion! wire x)
      (set! in-wires (list-set in-wires x wire)))

    (define (get-signal)
      (map (lambda (wire) (wire 'get-signal)) in-wires))

    (define (clear-data!)
      (set! data (make-gvector)))

    (define (add-newdata!)
      (gvector-add!
       data
       (apply
        vector
        (cons (sim-clock 'get-time) (get-signal)))))

    (define (init-scope!)
      (clear-data!)
      (add-newdata!))

    (define (add-data-to-results!)
      (sim-results 'add-sim-data! (gvector->vector data)))

    ;; reset is added last to be executed first
    (sim-clock 'add-init-sink-proc!  init-scope!)   
    (sim-clock 'add-sink-proc!       add-newdata!)
    (sim-clock 'add-end-proc!        add-data-to-results!)

    (lambda (msg . args)
      (case msg
        [(n-in)      n-in]
        [(n-out)     0]
        [(in-wires)  in-wires]

        [(data)               (gvector->vector data)]
        [(set-in-connexion!)  (apply set-in-connexion! args)]
        [else (error "Unkow operation SCOPE " msg)]))))

;; export all defined function
(provide (all-defined-out))

5.6. Alambres y conexiones

5.6.1. Alambres (wire)

El procedimiento make-wire crea un alambre. Un alambre es un objeto que mantiene un valor que se interpreta como el valor de una señal en un tiempo determinado.

Un alambre admite dos mensajes:

get-signal que devuelve el valor de la señal
set-signal! que recibe un valor y modifica el valor de la señal para que adquiera el valor recibido.

El procedimiento make-wires recibe n y crea una lista de n alambres. De hecho los bloques siempre se da mediante una lista de alambres aunque esa lista sólo contenga un alambre. El objeto que crea make-wires admite dos mensajes

get-signals que devuelve una lista de valores de los alambres.
set-signal! que recibe una lista de valores y modifica el valor almacenado en los alambres.

5.6.2. El alambre nulo null-wire

Cuando los bloques se crean, no se sabe como van a ser conectados, sin embargo es conveniente crear en ese momento los alambres de entrada y salida. Para ello se crean alambres nulos (null-wire). Un alambre nulo es un objeto cuyo valor siempre es cero. Un alambre nulo admite los mismos mensajes que un alambre normal pero ambos mensajes devuelven \(0.0\). El procedimiento make-null-wire crea un alambre nulo y el procedimiento make-null-wires crea una lista de alambres nulos. En seguida se presenta el código de make-null-wire y make-null-wires.

5.6.3. Conexiones (connexions)

Un alambre realiza una conexión (connexion) de un puerto (pto) de salida de un bloque a un puerto (pto) de entrada a otro bloque. Un puerto (pto) se representa con una lista de dos elementos: un bloque y un número. El número indica a cual de las entradas o salidas del bloque se refiere. La numeración de entradas y salidas de un bloque empieza de cero.

Una conexión (connexion) se representa con una lista de tres elementos: un puerto de salida de un bloque, un alambre y un puerto de entrada de otro bloque.

El procedimiento que realiza una conexión, esto es, conectar dos puertos se llama wire-up!. El procedimiento wire-up! recibe dos puertos, uno de salida de un bloque (oport) y otro de entrada a otro bloque (iport). wire-up! examina si ya existe un alambre que sale del oport, crea un alambre nuevo y realiza la conexión entre el oport y el iport. Si ya existiera un alambre que sale del oport entonces se utiliza el mismo alambre y solo se realiza la conexión al iport. En cualquier caso se agrega la connexion a una lista de connexions llamada sim-graph. El mantener esta lista permite saber si un oport ya ha sido conectado o no.

La conexión se realiza mandando a los bloques del oport e iport los mensajes de set-out-connexion! y set-in-connexion! respectivamente. Recuerde que estos mensajes requieren que se especifique el alambre y el número de puerto. La estructura de la instrucción es

(wire-up! oport iport)

Suponga que se quiere conectar la salida 1 del sistema sys a la entrada dos del osciloscopio scp, entonces la instrucción sería:

(wire-up! (pto sys 1) (pto scp 2))

Recuerde que las entradas y salidas de un bloque se numeran desde cero.

El procedimiento make-sim-graph crea un objeto que mantiene una lista de conexiones (connexions). Este objeto admite dos mensajes:

add-connexion! que agrega una conexión a la lista.
graph que devuelve la lista de conexiones.

Para una simulación se usa make-sim-graph para crear el objeto global sim-graph que mantiene la lista de conexiones del sistema.

El código para hacer alambres, alambres nulos y conexiones se muestra a continuación:

#lang racket

(require "../fnc/auxfnc.rkt")   ; general support functions

(define (make-wire)
  (let ([signal 0.0]) 

    (define (set-signal! val)
              (set! signal val))

    (lambda (msg . args)
      (case msg
          [(get-signal) signal]
          [(set-signal!) (apply set-signal! args)]
          [else (error "Unknown operation on WIRE " msg)]))))

;; The signal of a null-wire is zero and can not be changed
(define (make-null-wire)

    (lambda (msg . args)
      (case msg
          [(get-signal) 0.0]
          [(set-signal!) 0.0]
          [else (error "Unknown operation on NULL-WIRE " msg)])))


;; ========== wires ==========  
;; make a list of n wires
(define (make-wires n)
  (let ([wires (map0 make-wire  n)])

    (define (get-signals)
      (map (lambda (wire) (wire 'get-signal)) wires))
    
    (define (set-signals! vals)
      (for-each (lambda (wire val) (wire 'set-signal! val))
            wires vals))

    (lambda (msg . args)
      (case msg
          [(get-signals) (get-signals)]
          [(set-signals!) (apply set-signals! args)]
          [else (error "Unknown operation on WIRES " msg)]))))

(define (make-null-wires n)
  (let ([null-wires (map0 make-null-wire n)])

    (define (get-signals)
      (map (lambda (wire) (wire 'get-signal)) null-wires))
    
    (lambda (msg . args)
      (case msg
          [(get-signals) (get-signals)]
          [else (error "Unknown operation on NULL-WIRES " msg)]))))

;; ========== Block connexions ==========

;; Connexions are between ports.
;; A port is a list of one block and a number
(define (pto block [n 0])
  (list block n))

;; A connexion is a list of one oport a wire and an iport
;; connexion data: constructors and selectors
(define (make-connexion out w in)
  (list out w in))
(define (connexion-out connexion)
 (car connexion))
(define (connexion-wire connexion)
 (car (cdr connexion)))


(define (wire-up! oport iport)
  (let (
        [output-block (first oport)]
        [output-number (second oport)]
        [input-block (first iport)]
        [input-number (second iport)]
        [connexion (assoc oport (sim-graph 'graph))])

    (if (not connexion)
        (let ([wire (make-wire)])
          (output-block 'set-out-connexion! wire output-number)
          (input-block 'set-in-connexion! wire input-number)
          (sim-graph 'add-connexion! (make-connexion oport wire iport)))
        (let ([wire (connexion-wire connexion)])
          (input-block 'set-in-connexion! wire input-number)
          (sim-graph 'add-connexion! (make-connexion oport wire iport))))
    'wire-ok))

;; A sim-graph is a list of connexions
(define (make-sim-graph)
  (let ([graph null])

     (define (add-connexion! connexion)
      (set! graph (cons connexion graph)))
    
    (lambda (msg . args)
      (case msg
          [(add-connexion!) (apply add-connexion! args)]
          [(graph) graph]
          [else (error "Unknown operation on SIM-GRAPH " msg)]))))

(define sim-graph (make-sim-graph))

;; export all defined function
(provide (all-defined-out))

5.7. Procedimientos para el control de una simulación

5.7.1. El objeto sim-results

Si se quieren hacer simulaciones repetidas sin interrupción es conveniente guardar los resultados de cada simulación. El procedimiento make-sim-results crea un objeto que puede agregar resultados de simulación conforme se vayan generando. Cada resultado de una simulación es un elemento de un vector que puede crecer (gvector). Así cuando se genera un nuevo resultado de simulación se agrega al final de este vector. Un objeto creado con make-sim-results admite los siguientes mensajes:

clear-sim-data! Elimina los datos almacenados
add-sim-data! Agrega un nuevo resultado de simulación
sim-data Devuelve la lista de resultados almacenados.

Con el procedimiento make-sim-results se crea un objeto global llamado sim-results. Cada vez que termina una simulación cada osciloscopio transfiere sus datos a sim-results. El código se muestra aquí:

5.7.2. El objeto sim-prmtr

El procedimiento make-sim-prmtr crea un objeto que mantiene las variables:

init-time que almacena el tiempo inicial de simulación.
end-time que almacena el tiempo final de simulación.
dt que guarda el paso de integración.
int-method que guarda el algoritmo de integración.

Los objetos creados con make-sim-prmtr admiten los siguientes mensajes.

int-method informa el método de integración actual.
sim-time-prmtr devuelve una lista con tres elementos: el tiempo inicial de simulación, el tiempo final y el paso de integración.
set-interval! modifica el tiempo inicial y final de una simulación.
set-dt! modifica el paso de integración de una simulación.
set-int-method! establece o modifica el método de integración usado. La biblioteca utilizada tiene programada los siguientes tres métodos:
- rk2-ode-type metodo Runge-Kutta de orden 2,3.
- rk4-ode-type método de Runge-Kutta de orden 4.
- rkf45-ode-type método de Runge-Kutta de orden 4,5.

Con el procedimiento make-sim-results se crea el objeto global sim-prmtr que es conocido en todo el programa. El código se muestra aquí:

5.7.3. El procedimiento sim

El procedimiento sim realiza una simulación. Para ello extrae los datos de simulación de sim-prmtr. Manda el mensaje de inicialización al reloj y despues manda un tic al reloj hasta que se alcance el tiempo final final de simulación. Cuando el tiempo final es alcanzado se manda el mensaje de fin de simulación al reloj. aquí el código:

Todo el código para controlar la simulación se muestra a continuación

#lang racket
(require data/gvector)  ; sim-results uses growable vectors
(require (planet williams/science/ode-initval)) ; integration library

(require "../fnc/auxfnc.rkt")   ; general support functions
(require "clock.rkt")

;; ========== sim results ==========  
(define (make-sim-results)
  (let ([sim-data (make-gvector)])
    (define (clear-sim-data!)
      (set! sim-data (make-gvector)))
    (define (add-sim-data! new-sim-data)
      (gvector-add! sim-data new-sim-data))

    (lambda (msg . args)
      (case msg
        [(clear-sim-data!)  (clear-sim-data!)]
        [(add-sim-data!)    (apply add-sim-data! args)]
        [(sim-data)         (gvector->list sim-data)]
        [else (error "Unkow operation SIM-RESULTS " msg)]))))

(define sim-results (make-sim-results))

;; ========== sim parameters ==========  
(define (make-sim-prmtr)
  (let ([init-time   0.0]
        [end-time    80.0]
        [dt          0.02]
        ;; [int-method  rk2-ode-type]
        [int-method  rk4-ode-type]
        ;; [int-method  rkf45-ode-type]
        [max-state-val  1.0e+8]
        [min-state-val  -1.0e+8])
    
    (define (set-interval! t0 tf)
      (set! init-time t0)
      (set! end-time tf))

    (define (set-dt! new-dt)
      (set! dt new-dt))

    (define (set-int-method! new-method)
      (set! int-method new-method))

    (define (set-max-state-val! new-max-state-val)
      (set! max-state-val new-max-state-val))

    (define (set-min-state-val! new-min-state-val)
      (set! min-state-val new-min-state-val))

    (lambda (msg . args)
      (case msg
        ;; getters
        [(sim-time-prmtr)   (list init-time end-time dt)]
        [(int-method)       int-method]
        [(max-state-val)    max-state-val]
        [(min-state-val)    min-state-val]
        ;;; setters
        [(set-interval!)    (apply set-interval! args)]
        [(set-dt!)          (apply set-dt! args)]
        [(set-int-method!)  (apply set-int-method! args)]
        [(set-max-state-val!)          (apply set-max-state-val! args)]
        [(set-min-state-val!)          (apply set-min-state-val! args)]
        [else (error "Unknown operation on SIM-PRMTR" msg)]))))

(define sim-prmtr (make-sim-prmtr))

;; ==========  simulation ==========  
(define (sim)
  (let ([t0 (first   (sim-prmtr 'sim-time-prmtr))]
        [tf (second  (sim-prmtr 'sim-time-prmtr))]
        [dt (third   (sim-prmtr 'sim-time-prmtr))])
    (sim-clock 'init-sim!  t0 dt)
    (nl)
    (displayln "simulation in progress...")
    (define (loop ta)
      (if (>= ta tf)
          (begin
            (sim-clock 'end-sim!)
            (display "Done \n"))
          (begin
            (sim-clock 'tic!)
            (nl)
            (display (sim-clock 'get-time))
            (loop (sim-clock 'get-time)))))
    (loop t0)))

;; export all defined function
(provide (all-defined-out))

5.8. Conexiones comunes entre bloques

Es frecuente conectar bloques de cierta manera. por ejemplo se pueden conectar bloques en cascada (serie) o paralelo. Se pueden crear procedimientos para hacer automáticamente estas conexiones

5.8.1. Conexión en cascada de sistemas MIMO

El procedimiento cascade2 recibe dos bloques y crea un bloque compuesto como se muestra en la figura ??. El procedimiento revisa si el numero de salidas y entradas de los bloques permite la conexión. Si es así realiza las connexiones internas. El bloque compuesto sólo admite mensajes relativos a la conexión con otros bloques:

n-in
n-out
in-wires
out-wires
set-in-connexion!
set-out-connexion!

Si se quiere cambiar las expresiones que determinan el comportamiento de los bloques que integran al bloque compuesto, es necesario referirse a ellos directament.

Es importante observar que no se crean nuevos alambres de entrada y de salida, sino que las entradas al bloque compuesto son las entradas del primer y las salidas del bloque compuesto son las salidas del segundo bloque. Para lograr esto, los procedimientos set-in-connexion! y set-out-connexion! solo direccionan el mensaje al bloque 1 y al bloque 2 respectivamente. De esta manera se pueda hacer la aplicación repetida del procedimiento para conectar en cascada más de dos bloques.

El procedimiento cascade recibe una serie de bloques y los conecta en cascada mediante la aplicación repetida de cascade2. El código para la conexión en cascada se muestra a continuación.

5.8.2. Conexión de paralelo de sistemas SISO

El procedimiento parallel recibe dos o más bloques y los conecta en paralelo como se muestra en la figura ??. Para ello crea un bloque distribuidor y un bloque sumador y realiza las conexiones necesarias. La entrada del bloque compuesto es la del distribuidor y la salida es la del sumador.

El bloque compuesto admite las mismas mensajes que en el caso del procedimiento cascade. Si se quiere cambiar el comportamiento de los bloques no se puede hacer a través del bloque compuesto; se tiene que hacer directamente en cada uno de los bloques.

El código de la funciones cascade y parallel es el siguiente:

#lang racket

(require "../fnc/auxfnc.rkt")   ; general support functions
(require "wires.rkt")
(require "lib-static.rkt")

;; ========== cascade MIMO ==========  
;; cascade for two blocks
(define (cascade2 blck1 blck2)
  (let ([in-wires   (blck1 'in-wires)]
        [out-wires  (blck2 'out-wires)]
        [n-in       (blck1 'n-in)]
        [n-out      (blck2 'n-out)])
    
    (define (set-in-connexion! wire x)
      (blck1 'set-in-connexion! wire x))
    
    (define (set-out-connexion! wire x)
      (blck2 'set-out-connexion! wire x))
    
    (define (can-be-connected?)
      (= (blck1 'n-out) (blck2 'n-in)))
    
    (define (make-connexion!) 
      (map
       (lambda (pto-num)
         (wire-up! (pto blck1 pto-num) (pto blck2 pto-num) ))
       (range (blck1 'n-out)) ))
    
    (if (can-be-connected?)
        (make-connexion!)
        (error "blocks can not be connected"))    
    
    (lambda (msg . args)
      (case msg
        [(n-in)                n-in]
        [(n-out)               n-out]
        [(in-wires)            in-wires]
        [(out-wires)           out-wires]
        [(set-in-connexion!)   (apply set-in-connexion! args)]
        [(set-out-connexion!)  (apply set-out-connexion! args)]
        
        [else (error "Unknown operation on BLOCK " msg)]))))

;; ========== cascade for two o more blocks ==========  
(define (cascade . lst-blcks)
  (fold-binop cascade2 lst-blcks))

;; ========== parallel SISO ==========  

(define (parallel . lst-blcks)
  
  (let* ([n-in       1]
         [n-out      1]
         [n-blcks    (length lst-blcks)]
         [dstb       (make-distributor n-blcks)]
         [add        (make-adder n-blcks)]
         [in-wires   (dstb 'in-wires)]
         [out-wires  (add 'out-wires)])
    
    (define (set-in-connexion! wire x)
      (dstb 'set-in-connexion! wire x))
    
    (define (set-out-connexion! wire x)
      (add 'set-out-connexion! wire x))
    
    (define (can-be-connected?)
      (andmap (lambda (blck)
                (and (= (blck 'n-in) 1) (= (blck 'n-out) 1)))
              lst-blcks))
    
    (define (make-connexion!)
      (map (lambda (num)
             (wire-up! (pto dstb num)
                       (pto (list-ref lst-blcks num)))
             (wire-up! (pto (list-ref lst-blcks num))
                       (pto add num)))
           (range n-blcks)))
    
    (if (can-be-connected?)
        (make-connexion!)
        (error "blocks can not be connected"))    
    
    (lambda (msg . args)
      (case msg
        [(n-in)                n-in]
        [(n-out)               n-out]
        [(in-wires)            in-wires]
        [(out-wires)           out-wires]
        [(set-in-connexion!)   (apply set-in-connexion! args)]
        [(set-out-connexion!)  (apply set-out-connexion! args)]
        
        [else (error "Unknown operation on BLOCK " msg)]))))

;; ========== ==========  
;; export all defined function
(provide (all-defined-out))

5.9. Sistema de control clásico de una entrada una salida.

El procedimiento make-classic-retro-sys acepta dos bloques; el primero se refiere al sistema y el segundo al controlador; devuelve la estructura de la figura Con Sistema Típico. Note que si se tiene una secuencia de controladores o de sistemas, con este procedimiento se podrían hacer simulaciones repetidas.

El código de make-classic-retro-sys se prenseta a continuación

#lang racket

(require "sources.rkt")
(require "sinks.rkt")
(require "sim.rkt")
(require "wires.rkt")
(require "lib-static.rkt")
(require "../fnc/auxfnc.rkt")  

(define (sim-open-loop sys)
  (let ([src (make-step-src)]
        [scp (make-scope 2)])
  ;; wiring
  (wire-up! (pto src) (pto sys))
  (wire-up! (pto src) (pto scp 0))
  (wire-up! (pto sys) (pto scp 1))
  (sim)
  (scp 'data)))

(define (sim-classic-retro sys ctrl)
  (let ([src (make-step-src)]
        [scp (make-scope 2)]
        [diff (make-diff)])
  ;; wiring
  (wire-up! (pto src) (pto diff 0))
  (wire-up! (pto sys) (pto diff 1))
  (wire-up! (pto diff) (pto ctrl))
  (wire-up! (pto ctrl) (pto sys))

  (wire-up! (pto src) (pto scp 0))
  (wire-up! (pto sys) (pto scp 1))
  (sim)
  (scp 'data)))

;; export all defined function
(provide (all-defined-out))

6. Uso de esta biblioteca

Las funciones descritas permiten simular un gran número de sistemas dinámicos y ser aplicadas en un gran número de situaciones. Algunas de ellas se irán agregando a este documento en el futuro.

De entrada sugerimos examinar la implementación del algoritmo Optimización por enjambre de partículas y su aplicación en la sintonización de controladores descrito en este mismo sitio.

Date: Julio de 2022

Author: Domingo Cortés, Diego Martínez

Email: domingo.cortes@gmail.com

Validate

Simulador Programable de Sistemas Dinámicos en Racket