Sintonización de controladores usando PSO
Domingo Cortés, Christopher Morales
1. Introducción
En este documento se explica el desarrollo de un software que usa el algoritmo de conocido como Optimización por Enjambre de Particulas para la sintonización automática de controladores para sistemás dinámicos. El algoritmo de Optimización por Enjambre de Partículas se abrevia como PSO por las siglas de Particle Swarm Optimization.
El software descrito aquí, está desarrollado en racket que es una extensión del lenguaje de programación Scheme.
El documento está pensado para servir a cualquiera que inicie en programación para que pueda observar como se hace un software extenso. Así mismo los estudiantes de ingeniería pueden observar como los programar puede ayudarles a resolver problemas por ellos mismos sin depender de que exista o no un software comercial para ello.
2. Operaciones entre vectores y funciones
En esta sección se presentan procedimientos que facilitan la implementación del método de Optimización por Ejambre de Partículas (PSO) y su aplicación a la sintonización de controladores además de que son muy útiles en otras aplicaciones. Estos procedimientos realizan operaciones comunes entre vectores y funciones.
2.1. Determinando si un controlador es mejor que otro
En particular, los procedimientos desarrollados en este capítulo serán útiles para determinar si un controlador se desempeña mejor que otro. Para esto hay que definir de manera precisa que significa ``mejor'' y asociarle una calificación (número) a cada controlador. A este número en el PSO normalmente se le conoce como fitness. Coloquialmente hablando si un controlador es más adecuado que otro debería tener una calificación mas alta, es decir su fitness debería ser más grande. Sin embargo, al comparar controladores, es más sencillo evaluar una función de costo, así un controlador es mejor si el `costo' es menor. Aquí se usará ese costo su fitness y un controlador será mejor si tiene un fitness menor. Esto va en contrasentido con el lenguaje comunmente usado y quizá se debería usar una palabra distinta. En este documento se decidió usar la misma palabra y hacer la aclaración que un fitness menor es mejor.
Entre las ideas más comunes para definir ``mejor'' en lo que a controladores se refiere son:
- Una determinada norma del error.
- El máximo sobre impulso.
- El tiempo de establecimiento.
Cada uno de estos criterios arroja un número y eso permite comparar controladores.
Para usar estos criterios hay que programarlos. Dentro de las normas más usadas está la norma-2 definida por
\begin{equation} \| f \| = \left [ \int | f(x) |^{2} dx \right]^{1/2} \end{equation}A continuación, se desarrollan una serie de procedimientos para representar y calcular la norma-2 de funciones.
2.2. Representación de vectores y sus operaciones
Aunque en Racket existen bibliotecas para hacer operaciones comunes en algebra líneal, en este el código mostrado aquí se decidió no hacer uso de esas bibliotecas; principalmente, porque las operaciones que se requieren para desarrollar el PSO y su aplicación a la sintonización de controladores son sencillas y es mejor programarlas de forma directa en lugar de depender de una biblioteca.
Racket tiene una estructura de datos llamada vector y se usará esa estructura para representar los vectores necesarios en el programa. En el siguiente código se introducen algunos sinónimos útiles para acceder a los elementos de un vector. El más útil es vith para acceder al i-esimo elemento.
(define vith vector-ref) (define (vfirst v) (vith v 0)) (define (vsecond v) (vith v 1)) (define (vthird v) (vith v 2)) (define (vlast v) (vith v (sub1 (vector-length v))) )
La suma y resta de vectores es sólo la suma y resta de elementos. Obtener el negativo de un vector es sólo cambiar el signo a cada elemento. La multiplicación escalar es multiplicar cada elemento del vector por un número. Estas operaciones se denotan aquí como v+, v-, v-neg y v*; el siguiente código realiza estas operaciones:
(define (v+ v1 v2) (vector-map + v1 v2)) (define (v- v1 v2) (vector-map - v1 v2)) (define (v-neg v) (vector-map - v)) (define (v* v a) (vector-map (lambda (num) (* a num)) v))
El producto punto entre dos vectores es un escalar definido por. \[v_{a}\dot v_{b}= \sum_{i} v_{a_{i}} * v_{b_{i}} \] Para programar esta operación es conveniente definir v-sum-elmnts que toma los elementos de un vector y devuelve su suma. Con esta función es fácil expresar el producto punto (v.) y la magnitud (v-mag) que está dada por \(\norm{v}=v\dot v\)
(define (v-sum-elmnts v) (for/sum ([i v]) i)) (define (v. v1 v2) (v-sum-elmnts (vector-map * v1 v2))) (define (v-mag v) (sqrt (v. v v)))
2.3. Representación y operaciones entre funciones
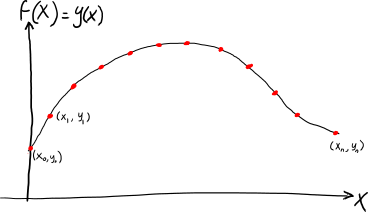
Para calcular numéricamente la norma de una función es necesario tener una representación de discreta de una función. Se puede ver a una función como una secuencia de pares ordenados \((x_{0},y_{0}), (x_{1},y_{1}), ... (x_{n},y_{n})\) (ver figura Representando una función discreta).
Una función también se puede representar como dos secuencias, una para los valores en el eje \(x\): \(x_{0},x_{1} ... x_{n}\); y otra para los valores en el eje \(y\): \(y_{0},y_{1} ... y_{n}\). Aquí se adopta esta última representación y se usan los vectores de la sección anterior para representar el dominio y el codiminio de una función discreta. Más precisamente una función discreta es un vector de dos vectores: uno para los valores del dominio (eje x) y otro para los valores del codominio (eje y).
El objeto para representar una función a partir de sus datos numéricos se llamará dfnc (discrete function). Para aislar el resto del programa de la representación de funciones, se hace un constructor y los selectores. Estos son:
(define (make-dfnc x fx) (vector x fx)) (define (x-dfnc dfnc) (vith dfnc 0)) (define (fx-dfnc dfnc) (vith dfnc 1))
Para hacer operaciones entre funciones se supone que ambas tienen el mismo dominio. Bajo esta suposición para sumar dos funciones se toman el dominio de cualquiera de ellas, y los valores de ambas funciones se suman como si fueran vectores. Esto se muestra en el código del procedimiento dfnc+ fueran vectores
;; dfnc add f1(x) + f2(x) (define (dfnc+ dfnc1 dfnc2) (make-dfnc (x-dfnc dfnc1) (v+ (fx-dfnc dfnc1) (fx-dfnc dfnc2))))
De una forma muy similar se realiza la resta de funciones ( dfnc- ), el negativo de una función (dfnc-neg) y el producto de una función por un escalar (dfnc*):
;; dfnc sub: f1(x) - f2(x) (define (dfnc- dfnc1 dfnc2) (make-dfnc (x-dfnc dfnc1) (v- (fx-dfnc dfnc1) (fx-dfnc dfnc2)))) ;; dfnc negative: -f(x) (define (dfnc-neg dfnc) (make-dfnc (x-dfnc dfnc) (v-neg (fx-dfnc dfnc)))) ;; scalar product: a(f(x)) (define (dfnc* dfnc a) (make-dfnc (x-dfnc dfnc) (v* (fx-dfnc dfnc) a)))
Un operador, recibe una función y devuelve otra. Los operadores que aplican una operación a cada elemento de la función se pueden programar de forma general de la siguiente manera
;; operation over a dfnc: op(f(x)) (define (dfnc-op dfnc op) (make-dfnc (x-dfnc dfnc) (vector-map op (fx-dfnc dfnc))))
Con dfnc-op es sencillo realizar muchas operaciones a una función discreta; por ejemplo el valor absoluto y el cuadrado de una función se pueden codificar así:
;; abs(f(x)) (define (dfnc-abs dfnc) (dfnc-op dfnc abs)) ;; sqr(f(x)) (define (dfnc-sqr dfnc) (dfnc-op dfnc sqr))
La función dfnc-int calcula la integral de una dfunc por el método del trapecio. Este método que consiste en aproximar el área bajo la curva de la función con trapecios (ver figura fig:trapecio). Si se suma el área de todos los trapecios se resulta que
o bien
\begin{equation} \int_{x_{0}}^{x_{n}} f(x) dx \approx \Delta_{x} \left[ \frac{f(x_{0})}{2} + \sum_{i=1}^{n-1}f(x_{i}) + \frac{f(x_{n})}{2} \right] \end{equation}que se puede escribir como
\begin{equation} \int_{x_{0}}^{x_{n}} f(x) dx \approx \Delta_{x} \left[ \sum_{i=1}^{n-1}f(x_{i}) - \left( \frac{f(x_{0})}{2} +\frac{f(x_{n})}{2} \right) \right] \end{equation}Esta expresión se puede codificar así:
;; trapezoidal integration method
(define (dfnc-int dfnc)
(let ([x (x-dfnc dfnc)]
[fx (fx-dfnc dfnc)])
(* (- (vsecond x ) (vfirst x)) ;; delta_x
(- (v-sum-elmnts fx)
(/ (+ (vfirst fx) (vlast fx)) 2.0))) ))
Con todos los procedimientos anteriores es sencillo calcular la norma-dos de una función discreta; se toma la función, se obtiene su valor absoluto, se eleva al cuadrado, se integra y finalmente se obtiene la raiz cuadrada. Esto es lo que hace el siguiente código:
;; norm2: sqrt( int( abs(f(x))^2 ) ) (define (norm2 dfnc) (sqrt (dfnc-int (dfnc-sqr (dfnc-abs dfnc)))))
El cálculo de la norma dos de una función discreta facilitará mucho asignar una medida desempeño, a cada controlador
3. Implementación del método de optimización por ejambre de partículas
3.1. El método de optimización por ejambre de partículas.
3.1.1. Idea general
El método de optimización por enjambre de partículas es un procedimiento herístico inspirado en el comportamiento de grupo en los animales observado en enjambres, rebaños, parvadas, cardúmenes, manadas, etc. Vea por ejemplo Parvada de pájaros.
Para no hablar de un grupo de animales en particular, se habla en general de un enjambre de partículas. Así, a este procedimiento se le conoce como Optimización por Enjambre de Partículas (Particle Swarm Optimization: PSO)
En la PSO se parte de generar de alguna manera un número de soluciones no óptimas. A cada una de estas soluciones se le considera como la posición de una partícula. Al conjunto de partículas se le considera un enjambre. La idea de la PSO es mover el enjambre para que sus partículas se vayan aproximando a una solución óptima. Mover el enjambre significa mover cada una de las partículas. Así cada partícula debe cambiar buscando que cada vez esté más cerca de la solución óptima.
3.1.2. Movimiento de las partículas
¿Qué significa mover una partícula? Recuerde que la posición de una partícula es una solución no óptima. Suponga que una solución (no óptima) de un problema está definida por un conjunto de parámetros. Est conjunto de parámetros define la posición de una partícula. Mover una partícula es cambiar su posición, es decir, cambiar sus parámetros buscando que después del cambio, la partícula esté más cerca de la solución óptima. Una idea trivial es mover la partícula en la dirección del óptimo. Sin embargo, no se conoce el óptimo y por lo tanto tampoco en que dirección está.
Otra idea es mover una partícula en todas direcciones y encontrar aquella dirección en que la función de costo disminuya en mayor medida. Es probable que ésta sea la dirección del óptimo. Eso es lo que se llama el método de la fuerza bruta y no se usa porque generalmente requiere un costo computacional enorme, aún en el caso de que cada solución sólo necesite unos pocos parámetros.
La PSO mueve cada partícula en la dirección que resulta de combinar tres direcciones:
- La dirección inercial. Suponga que la partícula se ha movido antes, entonces se puede calcular un vector velocidad que es la diferencia entre la posición actual y la última. La dirección inercial es la dirección del vector velocidad.
- La dirección cognitiva. Suponga qué se lleva el registro de la mejor posición que ha tenido la partícula. La resta de la mejor posición que ha ocupado la partícula y la posición actual es un vector que apunta hacia la mejor posición que ha ocupado la partícula. La dirección cognitiva es la dirección de este vector.
- La dirección social. Suponga que se lleva un registro de la mejor posición que ha ocupado el enjambre. La resta entre la mejor posición que ha ocupado el enjambre y la posición actual de la partícula es un vector que apunta hacia la mejor posición del enjambre. La dirección social es la dirección de este vector.
Si para la partícula \(i\) se define:
- \(x_{i}(k)\) La posición actual de la partícula.
- \(x_{i}(k-1)\) La posición previa de la partícula.
- \(x_{ib}(k)\) La mejor posición de la partícula hasta el momento.
- \(s_{b}(k)\) La mejor posición del enjambre hasta el momento.
entonces se puede calcular
- La dirección inercial: \(x_{i}(k)-x_{i}(k-1)\)
- La dirección cognitiva: \(x_{ib}(k)-x_{i}(k)\)
- La dirección social: \(s_{b}(k)-x_{i}(k)\)
Si escalamos estas direcciones por constantes, haciendo un símil con la física podemos hablar de velocidades, así tenemos
- La velocidad en la dirección inercial: \(v_{i_{inr}}(k)=w(x_{i}(k)-x_{i}(k-1))\)
- La velocidad en la dirección cognitiva: \(v_{i_{cgn}}(k)=k_{cog}(x_{ib}(k)-x_{i}(k))\)
- La velocidad en la dirección social: \(v_{i_{scl}}(k)=k_{scl}(s_{b}(k)-x_{i}(k))\)
donde \(w\), \(k_{cgn}\) y \(k_{scl}\) se conocen como constantes inercial, cognitiva y social respectivamente.
Se puede decir ahora que la partícula \(i\) se mueve a una velocidad
\begin{equation} \label{eq:vel} v_{i}(k)=v_{i_{inr}}(k) + v_{i_{inr}}(k) + v_{i_{inr}}(k) \end{equation}Así la posición de la partícula \(i\) en el instante \(k+1\) está dado por \(x_{i}(k+1)=x_{i}(k)+v_{i}(k)\). Poniendo esta expresión sólo en términos de posiciones resulta
\begin{equation} x_{i}(k+1) = x_{i}(k) w \left( x_{i}(k)-x_{i}(k-1) \right) + k_{cgn} \left( x_{ib}(k)-x_{i}(k) \right) + k_{scl} \left( s_{b}(k)-x_{i}(k) \right) \end{equation}Note que es conveniente expresar la siguiente posición en términos de posiciones anteriores (de la propia u otras partículas) ya que las posiciones son los parámetros de la soluciones (no óptimas) conocidas. Al mover una partícula estamos generando una nueva solución a partir de las soluciones conocidas.
Por alguna razón en la bibliografía en la expresión de la velocidad \ref{eq:vel} en lugar de \(v(k)\) se habla de \(v(k+1)\). Se considera aquí que no hay una justificación para ello.
En resumen la PSO podría describirse así (una mayor sangría significa subtarea). Dado un problema de optimización:
- Crear el enjambre
- Crear cada partícula
- Si no se cumpla la condición de paro
- Mover el enjambre
- Mover cada partícula
- Repetir
- Mover el enjambre
3.1.3. Ideas generales para la implementación del método
Para desarrollar un programa que implemente la PSO es conveniente pensar cuales son las palabras (ideas) principales del método. Podemos pensar en las siguientes expresiones:
- Enjambre
- Partícula
- Mover enjambre
- Mover partícula
- Mejor posición de la partícula
- Mejor posición del enjambre
- Generar posiciones iniciales
Note que en la descripción de la PSO se habló de un problema de optimización pero no se precisó cual es el problema. Esto es posible porque el método es bastante general. Para mantener esta generalidad en el programa es conveniente separar la implementación de la PSO de un problema particular. Para ello es necesario precisar que partes del procedimiento dependen del problema de optimización que se quiere resolver. La PSO necesita del 'problema' dos cosas
- La creación de partículas. Crear el enjambre significa crear partículas. Crear partículas es crear su posición inicial. La posición inicial de una partícula son los parámetros de una solución (no óptima) del problema. Es el 'problema' el que debe saber crear estas soluciones.
- Calcular el fitness. Se debe tener una medida de que tan buena es una partícula para resolver el problema. La medida más común es el valor de la función de costo que se desea minimizar (entre más pequeño mejor). A esta medida se le conoce aquí como el fitness. note que el fitness es un número real positivo. Para mover una partícula se necesita saber la mejor posición que la partícula ha tenido y la mejor posición que ha tenido el enjambre. Es decir se requiere saber si una posición es mejor que otra. Esta comparación se hace a través del fitness de cada posición, la que tenga menor fitness es mejor. El 'problema' debe saber como calcular el fitness asociado a una posición.
De las observaciones anteriores se puede expresar la SPO con las siguientes 'palabras'
- Problema
- Partícula
- Enjambre
- PSO
El 'Problema' debe poder crear posiciones no óptimas y calcular el fitnes de una posición.
Para que una partícula "se mueva", debe conocer además de su posición actual, su posición anterior y la mejor posición que ha ocupado hasta el momento. Note que la partícula debe conocer que es una 'mejor posición'. Esto se hace mediante el fitness. El cálculo del fitness le corresponde al 'problema'. Para no calcular el fitness de una posición varias veces es conveniente que a cada posición se le asocie su fitness. Llamaremos posfit a un par \((posición, fitness)\). Se tiene entonces que una partícula debe almacenar:
- El posfit actual
- El posfit previo
- El mejor posfit que ha tenido la partícula.
Para moverse, la partícula debe conocer también el mejor posfit del enjambre. El mejor posfit del enjambre es una propiedad del enjambre; así es el enjambre el que debe comunicar a cada particula cual ha sido su mejor posición. . En cada movimiento de la partícula se deben actualizar los tres posfit que componen la particula: el actual, el anterior, el mejor.
El enjambre contiene una lista de partículas y su mejor posfit hasta el momento. El enjambre debe poder moverse. Note que mover el enjambre significa mover cada una de sus partículas. En cada movimiento del enjambre debe actualizarse el mejor posfit del enjambre.
La PSO debe crear un enjambre y moverlo hasta que una condición de paro se cumpla. Crear un enjambre significa crear varias partículas. Crear partículas significa crear soluciones no óptimas.
Es conveniente guardar las constantes necesarias de la PSO en un sólo lugar. Esta información consiste en
- Número máximo de generaciones (movimientos del enjambre).
- Número de partículas del enjambre.
- Valor de la constante de inercia.
- Valor de la constante de cognitiva.
- Valor de la constante de social.
A continuación se presenta una implementación del método en el lenguaje de programación Racket.
3.2. Implementación de la PSO en Racket
3.2.1. Los datos necesarios para la ejecución del método
Hay un conjunto de funciones que no tienen que ver con el método que están programadas en 'auxfnc.rkt'. El método tambien requiere realizar operaciones con vectores. Estas operaciones están programadas en 'vfnc.rkt'. Finalmente se requieren procedimientos que dependen el problema. Estos procedimientos son make-potential-sol y calc-fitness. Las funciones de estos archivos se incorporan al PSO con las siguientes líneas.
(require "../fnc/auxfnc.rkt") (require "../fnc/vfnc.rkt") (require "../simpso/pso-ctrl-problem.rkt")
Las constantes del método están encapsuladas en una lista. Para extraerlas se usan selectores (getters). Esto se hace en las siguientes líneas
#;; ===== pso-data constructor and selectors ===== (define (make-pso-data max-generations num-particles k-inrt k-cgn k-scl) (list max-generations num-particles k-inrt k-cgn k-scl)) (define (max-generations pso-data) (list-ref pso-data 0)) (define (num-particles pso-data) (list-ref pso-data 1)) (define (k-inrt pso-data) (list-ref pso-data 2)) (define (k-cgn pso-data) (list-ref pso-data 3)) (define (k-scl pso-data) (list-ref pso-data 4))
Finalmente, es conveniente tener un función para mostrar los datos del método
(define (pso-data-display pso-data)
(let ([msgs (list "Máximo número de generaciones: "
"Número de particulas: "
"Constante inercial: "
"Constante social: "
"Constante cognitiva: ")])
(dp2l msgs pso-data)))
3.2.2. Creación y movimiento de partículas
Antes de crear las particulas es conveniente definir el dato posfit que es el par \((posición, fitness)\). El constructor y los selectores de posfit se muestra a continuación
;; ===== posfit constructor and selectors ===== (define (make-posfit pos fit) (list pos fit)) (define (pos posfit) (list-ref posfit 0)) (define (fit posfit) (list-ref posfit 1))
Una particula almacena una tripleta de posfit: su posfit actual, su posfit previo y su mejor posfit hasta el momento.
;; ===== particle constructor and selectors ===== (define (make-particle crrnt-posfit prev-posfit best-posfit) (list crrnt-posfit prev-posfit best-posfit)) (define (current-posfit particle) (list-ref particle 0)) (define (prev-posfit particle) (list-ref particle 1)) (define (best-posfit particle) (list-ref particle 2))
El procedimiento init-particle crea una partícula. Para ello, ejecuta los procedimientos:
make-potential-solque crea una solución no óptima del problema de optimización.calc-fitnesque recibe la posición de una partícula y devuelve su fitness
Estos dos procemientos dependen del problema y deben estar en un archivo aparte. Con el uso de estos procedimientos se crea una particula como se muestra a continuación. Note que al crear una particula, el posfit actual, el previo y el mejor son lo mismo.
(define (init-particle)
(let* ([pos1 (make-potential-sol)]
[fit1 (calc-fitness pos1)]
[posfit1 (make-posfit pos1 fit1)])
(make-particle posfit1 posfit1 posfit1)))
Para mover una particula es necesario conocer la mejor posición del enjambre hasta el momento y las constantes del método. Con ello se calculan las direcciones inercial, cognitiva y social y se multiplican por sus respectivas constantes. Con esto se calcula su nueva posición y a partir de la nueva posición se calcula el fitness. Con una nueva posición y un nuevo fitness se crea un nuevo posfit. Se examina si el nuevo posfit es mejor que el almacenado, si es así, entonces se actualiza el mejor posfit de la partícula. Esto es lo que se hace en las siguientes líneas
;; ===== move particle =====
(define (move-particle particle swrm-bst-pos pso-data)
(let ([ki (k-inrt pso-data)]
[kc (k-cgn pso-data)]
[ks (k-scl pso-data)]
[crrnt-posfit (current-posfit particle)]
[crrnt-pos (pos (current-posfit particle))]
[prev-pos (pos (prev-posfit particle))]
[best-pos (pos (best-posfit particle))]
[best-fit (fit (best-posfit particle))])
(define inrt-velocity (v* (v- crrnt-pos prev-pos) ki))
(define cgn-velocity (v* (v- best-pos crrnt-pos) kc))
(define scl-velocity (v* (v- swrm-bst-pos crrnt-pos) ks))
(define velocity
(v+ inrt-velocity (v+ cgn-velocity scl-velocity )))
(define new-pos (v+ crrnt-pos velocity))
(define new-fit (calc-fitness new-pos))
(define new-posfit (make-posfit new-pos new-fit))
(define new-best-posfit
(if (< new-fit best-fit) new-posfit crrnt-posfit ))
(make-particle new-posfit crrnt-posfit new-best-posfit)))
Es conveniente tener una función que muestre los datos de una partícula. En las siguientes líneas, se crea una lista de mensajes y una lista de variables. La función dp2l muestra cada mensaje con su correspondiente variable.
(define
(display-particle particle)
(let ([lst-msg (list
"posfit actual: "
"posfit anterior: "
"mejor posfit: ")]
[lst-var (list
(current-posfit particle)
(prev-posfit particle)
(best-posfit particle))])
(nl)
(dp2l lst-msg lst-var)))
3.2.3. Creación y movimiento del ejambre
En el dato swarm se ensamblan la lista de partículas y el mejor posfit del ejambre. A continuación el constructor y los selectores de este dato.
;; ===== swarm constructor and selectors ===== (define (make-swarm particles swarm-best-posfit) (list particles swarm-best-posfit)) (define (particles swarm) (list-ref swarm 0)) (define (swarm-best-posfit swarm) (list-ref swarm 1))
Para crear un ejambre, se crea una lista de partículas y se encuentra cual es el mejor posfit de esas partículas. El número de particulas a crear se conoce por los datos generales del método. El mejor posfit se encuentra usando la función update-swarm-best-posfit.
(define (init-swarm pso-data)
(let ([particles (map0 init-particle (num-particles pso-data))])
(update-swarm-best-posfit
(make-swarm particles (current-posfit (car particles))))))
Mover el ejambre equivale a mover cada partícula y después actualizar el mejor posfit del ejambre. Para mover una partícula se define el procedimiento auxiliar move-particle-crry que sólo requiere conocer la partícula en cuestión. Después este procedimiento se aplica a cada partícula de la lista. Para actualizar el mejor posfit del ejambre se usa el procedimiento update-swarm-best-posfit.
;; ===== move swarm =====
(define (move-swarm swarm pso-data)
(let([crrnt-bst-posfit (swarm-best-posfit swarm)]
[swrm-bst-pos (pos (swarm-best-posfit swarm))])
(define (move-particle-crry particle)
(move-particle particle swrm-bst-pos pso-data))
(define new-particles
(map move-particle-crry (particles swarm)))
(update-swarm-best-posfit
(make-swarm new-particles crrnt-bst-posfit))))
Después de crear el ejambre y despúes de cada movimiento se require actualizar el mejor posfit del ejambre. Esto se hace con la función update-swarm-best-posfit. Esta función utiliza la función auxiliar compare-posfit que que recibe una partícula y un posfit.
(define (compare-posfit particle bst-posfit)
(let ([crrnt-posfit (current-posfit particle)]
[fit-particle (fit (current-posfit particle))]
[bst-fit (fit bst-posfit)])
(if (< fit-particle bst-fit) crrnt-posfit bst-posfit)))
(define (update-swarm-best-posfit swarm)
(let* ([crrnt-particles (particles swarm)]
[crrnt-bst-posfit (swarm-best-posfit swarm)]
[new-best-posfit
(foldl compare-posfit crrnt-bst-posfit crrnt-particles)])
(make-swarm crrnt-particles new-best-posfit)))
Es conveniente tener una función que muestre el ejambre; esto es que muestre cada partícula del ejambre y el mejor posfit del ejambre
(define (display-swarm swarm) (for-each display-particle (particles swarm)) ( dp2 "mejor posfit de ejambre:" (swarm-best-posfit swarm)))
3.2.4. Ejecutando la PSO
La función evolve-swarm recibe un ejambre y los datos de la PSO. Esta función mueve el ejambre durante el número de iteraciones especificado por los datos de la PSO.
(define (evolve-swarm swarm pso-data)
(define (move-swarm-aux num swarm)
(nl)
(dp "Moving Swarm...: ")
(display-swarm swarm)
(move-swarm swarm pso-data))
(foldl move-swarm-aux swarm (range (max-generations pso-data))))
Finalmente, la función pso recibe el dato pso-data con la especificación de las constantes del método, crea un ejambre inicial y despues lo mueve usando evolve-swarm.
(define (pso pso-data)
(let ([iswrm (init-swarm pso-data)])
(dp "Swarm inicial: ")
(display-swarm iswrm)
(evolve-swarm iswrm pso-data))
)
;; export all defined function
(provide (all-defined-out))
3.3. Evaluación del método con un problema de prueba.
Como se ha mencionado, la PSO se puede aplicar a una diversidad de problemas. La parte del programa que tiene que ver con el problema debe proporcionar dos funciones:
make-potential-solque no recibe ningún argumentocal-fitnesque recibe una posición.
A continuación se presenta el código necesario para encontrar el mínimo de la función \[ f(x,y) = x^{2} + y^{2} - xy -3x + 4y -5 \]
Primero se crea el dato pos compuesto de un vector de dos elementos
(define (make-pos x1 x2) (vector x1 x2)) (define (x1-pos pos) (vith pos 0)) (define (x2-pos pos) (vith pos 1))
Una partícula es una posible solución del problema; en este caso es un par de números aleatorios en el intervalo \([-10,10)\). Con estos números se crea la posición (pos) de la partícula
(define (make-potential-sol) (make-pos (rnd -10 10) (rnd -10 10)))
Finalmente el fitness asociado a una partícula es directamente el valor de la función de costo. Estas funciones deben de conocerse por la PSO.
(define (calc-fitness pos)
(let ([x (x1-pos pos)]
[y (x2-pos pos)])
(+ (sqr x) (sqr y) (* (- x) y) (* -3 x) (* 4 y) -5)))
;; export all defined function
(provide (all-defined-out))
En un archivo aparte se introduce el siguiente código que especifica que la PSO ha de correrse con los datos:
- Número de iteraciones: \(50\)
- Número de partículas: \(10\)
- Constante inercial: \(0.7\)
- Constante cognitiva: \(0.5\)
- Constante social: \(0.3\)
Con estos datos se aplica la PSO y se muestran los resultados
(require "../fnc/auxfnc.rkt") (require "pso.rkt") ;; test pso-data (define datos-pso (make-pso-data 50 10 0.7 0.5 0.3)) (define resultado (pso datos-pso)) (nl) (dp "Resultados:") (display-swarm resultado)
En cada corrida el swarm inicial es distinto. Algunas particulas típicas del ejambre inicial se ven así:
Swarm inicial: posfit actual: (#(3.2160115216230984 -8.736409814370154) 65.17030735012128) posfit anterior: (#(3.2160115216230984 -8.736409814370154) 65.17030735012128) mejor posfit: (#(3.2160115216230984 -8.736409814370154) 65.17030735012128) posfit actual: (#(-1.297259789386306 4.399948440303394) 43.24187855483795) posfit anterior: (#(-1.297259789386306 4.399948440303394) 43.24187855483795) mejor posfit: (#(-1.297259789386306 4.399948440303394) 43.24187855483795) posfit actual: (#(-5.542724927162468 8.449885905155977) 194.38548306863999) posfit anterior: (#(-5.542724927162468 8.449885905155977) 194.38548306863999) mejor posfit: (#(-5.542724927162468 8.449885905155977) 194.38548306863999) posfit actual: (#(6.017920591805009 8.710005211569623) 71.44969838827043) posfit anterior: (#(6.017920591805009 8.710005211569623) 71.44969838827043) mejor posfit: (#(6.017920591805009 8.710005211569623) 71.44969838827043) posfit actual: (#(9.474802150102065 -4.469163787920509) 100.78868181179797) posfit anterior: (#(9.474802150102065 -4.469163787920509) 100.78868181179797) mejor posfit: (#(9.474802150102065 -4.469163787920509) 100.78868181179797)
Después de 50 iteraciones el enjambre final típico resulta:
Resultados: posfit actual: (#(0.6666602513011697 -1.666665933724397) -9.333333333286937) posfit anterior: (#(0.6666595957942975 -1.6666653846048598) -9.333333333272627) mejor posfit: (#(0.6666595957942975 -1.6666653846048598) -9.333333333272627) posfit actual: (#(0.6666666225444253 -1.6666621495305827) -9.333333333312726) posfit anterior: (#(0.6666701803706316 -1.6666605881185939) -9.333333333305397) mejor posfit: (#(0.6666666225444253 -1.6666621495305827) -9.333333333312726) posfit actual: (#(0.6666612648580171 -1.666657016789357) -9.333333333158908) posfit anterior: (#(0.6666583498217651 -1.6666521643380299) -9.333333332933233) mejor posfit: (#(0.6666612648580171 -1.666657016789357) -9.333333333158908) . . . posfit actual: (#(0.6666613781864857 -1.666669721293272) -9.33333333331219) posfit anterior: (#(0.6666672343173263 -1.6666661367303721) -9.33333333333303) mejor posfit: (#(0.6666672343173263 -1.6666661367303721) -9.33333333333303) posfit actual: (#(0.6666523765515237 -1.6666606781929203) -9.333333333007687) posfit anterior: (#(0.6666498498080317 -1.6666588262265964) -9.333333332857203) mejor posfit: (#(0.6666498498080317 -1.6666588262265964) -9.333333332857203) mejor posfit de ejambre:(#(0.6666672343173263 -1.6666661367303721) -9.33333333333303)
Note que todas las partículas están concentradas en el mínimo de la función.
4. Aplicación del PSO a problemas de control
4.1. Introducción
Para aplicar el PSO a la sintonizacion de algoritmos de control en necesario precisar el sistema que se quiere controlar, el tipo de referencia, el esquema de control y la estructura del controlador.
En esta tésis se aborda el esquema de la figura Esquema clásico de control. En principio la referencia podría ser de cualquier tipo; el sistema podría ser de cualquier orden y la estructura del controlador podría ser cualquiera. Sin embargo, en esta tesis se supone que la referencia es constante y que el controlador es un controlador clásico. Esto es, el controlador es uno de los siguientes controladores:
- Proporcional - integral (PI)
- Proporcional - derivativo (PD)
- Porporcional - integral - derivativo (PID)
- Compensador de adelanto - atraso
Se supone que el sistema es un sistema que puede ser controlado por estos controladores y se requiere es sintonizarlo.
Para aplicar el pso en esta situación se supone que los parámetros de un controlador definen la posición de una partícula. El ejambre, como conjunto de partículas es entonces un conjunto de controladores. Crear un ejambre significa crear un conjunto de controladores al azar. Mover el ejambre en esta analogía significa crear nuevos controladores a partir de los controladores existentes usando las reglas para el movimiento de las particulas del PSO.
Para ello es necesario conocer el fitness de cada controlador, esto es, tener alguna manera de calificar que tan bueno es un controlador. Aquí se calificará cada controlador en base a la norma dos del error entre la salida del sistema y la referencia. Un mejor controlador será el que arroje una menor norma del error. Conocer la norma del error de cada controlador implica simular cada controlador (partícula) del ejambre.
En resumen para aplicar el PSO a la sintonización de controladores clásicos se requiere:
- Crear el ejambre. Lo cual quiere decir crear al azar un conjunto de controladores; como un controlador está definido por sus parámetros, crear un controlador al azar quiere decir generar al azar sus parámetros. En general es necesario especificar un rango dentro de los cuales estén los parámetros del controlador. Este rango se establece de forma herística.
- Calcular el fitness de cada controlador. Esto es simular cada controlador y calcular la norma dos del error.
La generación de controladores al azar se reduce entonces a la generación de números al azar dentro de un rango. Sin embargo, la simulación de cada controlador no es tan sencilla, pues debe ocurrir de forma automática para que la PSO se ejecute sin intervención del usuario. Para la simulación de cada controlador se usará el simulador construido en [??Diego]. El uso de este controlador y su adaptación para usarlo en el PSO se describe a continuación.
4.2. Simulando de controladores de forma automática
El simulador al que se refiere esta sección está descrito en este mismo sitio. Por favor, refierase a la descripción y programación del simulador para conocer todos los detalles. Aquí se menciona como adaptar este simulador para ser usado en la PSO.
4.2.1. Descripción general del simulador
El simulador no esta desarrollado para un usuario final sino como una herramienta de investigación. Para poder utilizarlo es necesario saber programar en Scheme/Racket pues la representación de un sistema se hace en este lenguaje de programación.
Para construir una representación de un sistema de control se especifican los bloques que lo forman. El simulador tiene una característica que hace que se puedan simular un gran numero de controladores sin intervención: separa la conexión de la especificación de los bloques. Esto se explica a continuación
Suponga que se quiere construir un esquema clásico de control como el que se muestra en la figura Esquema clásico de control
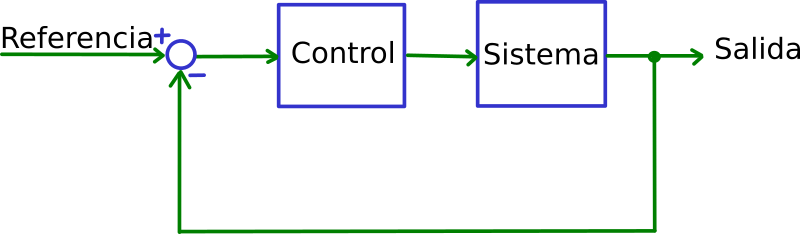
Figure 1: Esquema clásico de control
Entonces se puede describir la conexion así:
- conecta la fuente con la entrada positiva del restador
- conecta la salida del restador con el controlador
- conecta la salida del controlador con el sistema
- Conecta la salida del sistema con la entrada negativa del restador
Estas conexiones se pueden 'empaquetar' en un procedimiento, de tal manera que el procedimiento puede recibir la fuente, el controlador y el sistema y realizar la conexión. Más aún, si en una serie de simulaciones, la fuente y el sistema no cambian, se puede crear un procedimiento particular, que sólo reciba el controlador y realice la conexión de forma automática. No solo eso, también se puede crear un procedimiento que realice la conexión, haga la simulación y calcule la norma dos del error de un controlador determinado.
A continuación se presentan algunas funciones del simulador que son importantes para poder aplicar el PSO.
4.2.2. Conexiones
La figura 2 muestra como están conceptualizadas las conexiones entre bloques en el simulador. Las entradas y salidas de los bloques están numeradas. Estas entradas y salidas se conocen como puertos el primer puerto siempre es cero. Las conexiones siempre van de un puerto de salida de un bloque a un puerto de entrada de otro bloque. Para realizar una conexión se deben especificar ambos puertos. El siguiente código hipotético realizaría una conexión entre el puerto 1 de salida de bloque A y el puerto 0 de entrada del bloque B.
(wire-up! (pto bloqueA 1) (pto bloqueB 0))
Cuando el puerto es el puerto cero de cualquier bloque, éste se puede omitir. Esto es útil porque muchos bloques sólo tienen un puerto de entrada o de salida. Así, el codigo anterior también pudo haberse escrito como
(wire-up! (pto bloqueA 1) (pto bloqueB))
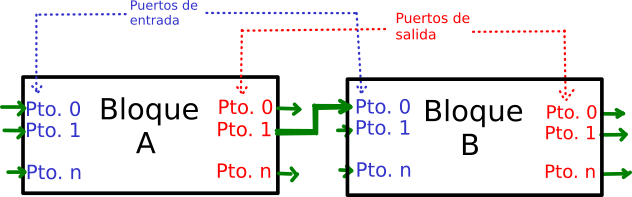
Figure 2: Conexión entre dos bloques
A continuación se describen los bloques que se usaron
4.2.3. Bloques del simulador usados
El el simulador un sistema de control se representa mediante la interconexión de bloques. Estos bloques actualizan sus entradas y salidas en cada 'tic' de un reloj que los sincroniza. El simulador tiene implementado los siguientes bloques:
4.2.3.1. Bloque estático
Este bloque puede tener \(n\) entradas y \(m\) salidas e implementa una función estática \(f:R^{n}\to R^{m}\). Aquí sólo se usa el restador como bloque estático. Este bloque implementa la función \(f(u_{1},u_{2}) = u_{1}-u_{2}\) donde \(u_{1}\) y \(u_{2}\) son las entradas del bloque. El código relevante para este bloque es:
;; error block: substract two signals
(define (make-diff)
(let ([sub (make-static-sys 2 1)])
(sub 'set-in-symb! '(u1 u2))
(sub 'set-prmtr-symb! '())
(sub 'set-out-expr! '((- u1 u2)))
sub))
(define diff (make-diff))
4.2.3.2. Bloque de fuente.
Este bloque implementa un función del tiempo que usualmente sirve como referencia. El reloj de la simulación puede informar a todos los bloques el tiempo de simulación, por ello, no es necesario que ningún bloque tenga el tiempo como entrada. Así el bloque de fuente no tiene ninguna entrada, sólo salidas. En principio un bloque de fuente puede tener \(m\) salidas. Aquí sólo se usará un bloque que implementa el escalón unitario. Este bloque se cofidifica así:
(define (make-step-src [val 1.0])
(let ([step-src (make-src)])
(step-src 'set-prmtr-symb! '(k))
(step-src 'set-out-expr! '((k)))
(step-src 'set-prmtr-val! (list val))
step-src))
(define src (make-step-src))
4.2.3.3. Bloque de scope
Este bloque puede tener \(n\) entradas y no tiene salidas. Almacena el valor de sus entradas en cada 'tic' del reloj, de tal manera que después se puedan graficar o utilizar para postprocesamiento. Aquí se utiliza un scope de dos entradas para almacenar la referencia y la salida del sistema en cada simulación; el código que lo hace es el siguiente:
(define scp (make-scope 2))
4.2.3.4. Bloque de sistema dinámico
Este bloque puede tener \(n\) entradas y \(m\) salidas. Aquí los bloques de sistemas dinámicos utilizados tienen sólo una entrada y una salida. Para especificar un sistema dinámico es necesario definir:
- Qué símbolos se deben interpretar como parámetros
- Qué símbolos se deben interpretar como estados
- Qué simbolos se deben interpretar como salidas
- Las expresiones de los estados
- Las expresiones de la salida
- Los valores de los parámetros
- Las condiciones iniciales de los estados.
Para ilustrar como se representa un sistema dinámico en el simulador, el modelo de un péndulo simple dado por:
\begin{align} \dot x_{1} &= x_{2} \\ \dot x_{2} &= -\frac{g}{l}\sin(x_{1}) + \frac{\tau}{ml^{2}} \end{align}se representaría en el simulador por
;; Modelo del pendulo simple
(define (make-pendulo m g l [ic 0.0 0.0])
(define pendulo (make-dynsys 1 1))
(pendulo 'set-state-expr! '( (x2)
(+ (* (/ (- g) l) (sin x1)) (/ tau (* m l l)) )))
(pendulo 'set-out-expr! '( (x1)) )
(pendulo 'set-state-symb! '(x1 x2))
(pendulo 'set-prmtr-symb! '(m g l))
(pendulo 'set-init-cond! (list ic))
(pendulo 'set-in-symb! '(tau) )
(pendulo 'set-prmtr-val! (list m g l) )
pendulo)
Después del código anterior se podría generar la representación de un péndulo simple con la instrucción:
(define un-pendulo (make-pendulo 1 1 1))
4.2.4. Simulando un sistema de retroalimentación clásica
4.2.4.1. El esquema clásico de control
Un esquema clásico de control se muestra en la figura 1. Se puede representar y simular este esquema de control usando los bloques descritos anteriormente. El siguiente código define un procedimiento que recibe un (bloque de un) sistema y un (bloque de un ) controlador y devuelve los datos de la simulación del sistema que incluye un vector de valores de tiempo y los valores de la referencia y salida en esos tiempos. El procedimiento crea internamente una fuente src, un scope scp, un restador diff alambra los bloques y realiza la simulación. En este procedimiento se puede observar la ventaja de que el simulador sea programable, es decir que permita definir procedimientos repetitivos en simulación. En particular este procedimiento automatiza la simulación del esquema de la figura 1.
(define (sim-classic-retro sys ctrl) (define src (make-step-src)) (define scp (make-scope 2)) (define diff (make-diff)) ;; wiring (wire-up! (pto src) (pto diff 0)) (wire-up! (pto sys) (pto diff 1)) (wire-up! (pto diff) (pto ctrl)) (wire-up! (pto ctrl) (pto sys)) (wire-up! (pto src) (pto scp 0)) (wire-up! (pto sys) (pto scp 1)) (sim) (scp 'data))
Los bloques del control ctrl y del sistema sys dependen del sistema que se quiera controlar y del tipo de controlador que se quiera sintonizar. A continuación se explica como se representa en el simulador cada uno de los controladores clásicos considerados en el ejemplo que aquí se desarrolla.
4.2.4.2. Simulación del controlador Proporcional-Integral
La función de transferencia del controlador Proporcional-Integral (PI) está dada por
\begin{equation} G(s)=k_{p} + \frac{k_{i}}{s} = \frac{k_{p}s + k_{i}}{s} \end{equation}Hay varias representaciones de estado que tendrían la función de transferencia de un controlador PI. A una representación de estado que tiene una función de transferencia determinada se le conoce como una realización de esa función de transferencia. En [??ogata] se describe como obtener varias realizaciones para una función de transferencia. Aquí se emplea la realización en forma canónica controlable para todos los controladores utilizados.
Siguiendo el procedimiento descrito en [??ogata] Una realización del controlador PI está dada por el sistema dinámico
\begin{align} \dot x &= u \\ y &= k_{i} x + k_{p} u \end{align}Este sistema dinámico se puede representar en el simulador con el siguiente código
;; PI controller. (define (make-PI kp ki [ic 0.0]) (define PI (make-dynsys 1 1)) (PI 'set-state-expr! '( (u) )) (PI 'set-out-expr! '( (+ (* ki x ) (* kp u)) ) ) (PI 'set-state-symb! '(x)) (PI 'set-prmtr-symb! '(kp ki)) (PI 'set-init-cond! (list ic)) (PI 'set-in-symb! '(u) ) (PI 'set-prmtr-val! (list kp ki) ) PI)
Con este código es muy sencillo crear un controlador PI a partir de sus parámetros.
4.2.4.3. Simulación del controlador Proporcional-Derivativo
La función de transferencia ideal del controlador Proporcional-Derivativo esta dada por
\begin{equation} G(s)=k_{p} + k_{d} s \end{equation}Sin embargo, por cuestiones prácticas, no es deseable intentar construir una función de transferencia así. Generalmente a esta función de transferencia se le agrega un filtro de primer orden para eliminar las altas frecuencias. La función de transferencia del controlador PD queda entonces
\begin{equation} G(s)=k_{p} + \frac{ k_{d} s}{s+a} = \frac{(k_{p}+k_{d})s + k_{p}a}{s+a} \end{equation}donde el valor del polo \(a\) es mayor que \(k_{d}\).
Siguiendo el procedemiento descrito en diversos libros de control, por ejemplo el de Ogata, una realización del controlador PD es
\begin{align} \dot x &= -a x + u \\ y &= -a k_{d} x + k_{p} k_{d} u \end{align}Este sistema dinámico se puede representar en el simulador con el siguiente código
;; PD controller. kp, kd, a are the controller constants ;; a is the pole of de controller first order filter (define (make-PD kp kd a [ic 0.0]) (define PD (make-dynsys 1 1)) (PD 'set-state-expr! '( (+ (* (- a) x) u) ) ) (PD 'set-out-expr! '( (+ (* (- a) kd x) (* (+ kp kd) u)) ) ) (PD 'set-state-symb! '(x)) (PD 'set-prmtr-symb! '(kp kd a)) (PD 'set-init-cond! (list ic)) (PD 'set-in-symb! '(u) ) (PD 'set-prmtr-val! (list kp kd a) ) PD)
Este procedimiento facilita mucho crear un controlador PD a partir de sus parámetros.
En el ejemplo que estamos desarrollando, en la sintonización del PD se utiliza un valor para \(a\) de \(10\) veces \(k_{d}\), es decir \(a=10k_{d}\). Se podría no ligar el valor de \(a\) al valor de \(k_{d}\), de tal manera que se sintonizara también \(a\). Pero eso sería equivalente a sintonizar una compensador de atraso/adelanto, y eso ya está contemplado en otro controlador.
4.2.4.4. Simulación del controlador Proporcional-Integral-Derivativo
La función de transferencia del controlador Proporcional-Integral-Derivativo (PID) está dada por
\begin{equation} G(s)=k_{p} + \frac{ k_{d} s}{s+a} + \frac{k_{i}}{s} \end{equation}o bien
\begin{equation} G(s)= \frac{(k_{p}+k_{d})s^{2} + (a k_{p} + k_{i})s + ak_{i}} {s(s+a)} \end{equation}Una realización del controlador PID es
\begin{align} \dot x_{1} &= x_{2} \\ \dot x_{2} &= -a x_{2} + u \\ y &= a k_{i} x_{1} + (k_{i}-ak_{d})x_{2} + (k_{p} + k_{d})u \end{align}Este sistema dinámico se puede representar en el simulador con el siguiente código
;; PID controller. kp, ki, kd, a are the controller constants
;; a is the pole of de controller first order filter
(define (make-PID kp ki kd a [ic '(0.0 0.0)])
(define PID (make-dynsys 1 1))
(PID 'set-state-expr!
'( (x2)
(+ (* (- a) x2) u) ))
(PID 'set-out-expr! '( (+ (* a ki x1)
(* (- ki (* a kd) ) x2)
(* (+ kp kd) u) ) ) )
(PID 'set-state-symb! '(x1 x2))
(PID 'set-prmtr-symb! '(kp ki kd a))
(PID 'set-init-cond! ic)
(PID 'set-in-symb! '(u) )
(PID 'set-prmtr-val! (list kp ki kd a) )
PID)
Con este procedimiento se puede crear facilmente un controlador PID a partir de sus parámetros.
4.2.4.5. Simulación del compensador de atraso/adelanto
Un compensador de atraso y uno de adelanto tienen la misma función de transferencia
\begin{equation} G(s)=k_{c} \frac{s + z_{c}}{s+p_{c}} \end{equation}Lo que los distingue es la ubicación del polo y el cero. En el de atraso domina el polo \(p_{c}
Siguiendo el mismo procedimiento que para los controladores anteriores se obtiene la realización del compensador de atraso/adelanto dada por
\begin{align} \dot x &= - p_{c} x + u \\ y &= k_{c}( z_{c} - p_{c} )x + k_{c} u \end{align}En el simulador, el compensador atraso/adelando se puede representar con el código
(define (make-compensator kc zc pc [ic 0.0])
(define COMP (make-dynsys 1 1))
(COMP 'set-state-expr! '( (+ (* (- pc) x) u) ) )
(COMP 'set-out-expr! '( (+ (* kc (- zc pc) x)
(* kc u)) ) )
(COMP 'set-state-symb! '(x))
(COMP 'set-prmtr-symb! '(kc zc pc))
(COMP 'set-init-cond! (list ic))
(COMP 'set-in-symb! '(u) )
(COMP 'set-prmtr-val! (list kc zc pc) )
COMP)
Este procedimiento permite crear fácilmente un compensador de atraso/adelanto a partir de sus parámetros.
4.2.5. Simulando sistemas dinámicos
La simulación de los controladores clásicos muestra como se representan sistemas dinámicos en el simulador. También se ha mostrado que se pueden hacer procedimientos para hacer conexiones de forma automática. De la misma manera se pueden representar sistemas dinámicos generales y luego obtener representaciones particulares. Por ejemplo, para representar el sistema lineal de segundo orden expresado por
\begin{equation} \dot x = Ax + bu \; \qquad y = cx + du \end{equation}donde \(A\) es una matrix de \(2\times 2\), \(b\) es un vector de \(2\times 1\), \(c\) es un vector de \(1\times 2\) y \(d\) es un escalar, se puede usar el código
(define (make-slo2 a b c [d 0] [ic '(0.0 0.0)])
(define sys (make-dynsys 1 1))
(let ([a11 (list-ref a 0)] [a12 (list-ref a 1)]
[a21 (list-ref a 2)] [a22 (list-ref a 3)]
[b1 (list-ref b 0)] [b2 (list-ref b 1)]
[c1 (list-ref c 0)] [c2 (list-ref c 1)])
;; system definition
(sys 'set-state-expr! '( (+ (* a11 x1) (* a12 x2) (* b1 u) )
(+ (* a21 x1) (* a22 x2) (* b2 u) ) ))
(sys 'set-out-expr! '( (+ (* c1 x1) (* c2 x2) (* d u)) ))
(sys 'set-state-symb! '(x1 x2))
(sys 'set-prmtr-symb! '(a11 a12 a21 a22 b1 b2 c1 c2 d))
(sys 'set-init-cond! '(0.0 0.0))
(sys 'set-in-symb! '(u) )
(sys 'set-prmtr-val! (list a11 a12 a21 a22 b1 b2 c1 c2 d) )
sys))
Una vez teniendo este procedimiento se pueden crear sistemas de segundo orden, especificando sólamente las listas de coeficientes a, b, c y d. Si no se especifica d se le asigna \(0\). Este código se utiliza en uno de los ejemplos.
De la misma manera se podría simular estructuras generales y a partir de ellas generar sistemas particulares.
4.3. Aplicando el PSO a la sintonización de controladores
4.3.1. Cálculo del fitness de una partícula
Una vez conociendo como se simula un esquema clásico de retroalimentación a partir de sus bloques y teniendo procedimientos para generar controladores clásicos a partir de sus parámetros, se puede construir un procedimiento que dado un sistema:
- Reciba los parámetros del controlador clásico.
- Construya (realice las conexiones) el esquema clásico del control.
- Realice la simulación.
- Obtenga la señal del error
- Calcule la norma dos de la señal de error.
Es decir, en términos del PSO, este procedimiento recibiría la posición de una partícula (los parámetros del controlador) y devolvería su fitness. Como se recordará, es el cálculo del fitness el procedimiento que faltaba para aplicar el PSO la sintonización de controladores.
A continuación se muestran algunos ejemplos de la aplicación del PSO a la sintonización de controladores.
4.3.2. Sintonización de un PD para el sistema de segundo orden
En este ejemplo se sintonizará un controlador PD para el sistema con función de transferencia
\begin{equation} G(s) = \frac {1}{s(s+1)} \end{equation}Una realización de este sistema esta dado por
\begin{equation} \dot x = \begin{bmatrix} 0 & 1 \\ 0 & -1 \end{bmatrix} x + \begin{bmatrix} 0 \\ 1 \end{bmatrix} u \ ; \quad y = \begin{bmatrix} 1 & 0 \end{bmatrix}u \end{equation}Usando el procemiento make-slo2 definido arriba, este sistema se puede representar con el código
(define a1 '(0.0 1.0 0.0 -1.0)) (define b '(0.0 1.0)) (define c '(0.1 0.0)) (define sys1 (make-slo2 a1 b c))
Se sabe [??Ogata] que en un controlador La constante proporcional y derivativa del controlador son positivas. Además, por lo general la constante proporcional es mayor que la constante derivativa. Teniendo en cuenta esto para generar una particula (controlador) al azar se generan dos números aleatorios; el primero (\(k_{p}\)) está en \([0,20]\) y el segundo (\(k_{d}\)) en \([0,10]\). El código código para generar partículas (controladores) al azar queda
(define (make-pos x1 x2)
(vector x1 x2))
(define (x1-pos pos)
(vith pos 0))
(define (x2-pos pos)
(vith pos 1))
(define (make-potential-sol)
(make-pos (rnd 0.0 20.0)
(rnd 0.0 10.0)))
El siguiente procedimiento sim-pd-ctrl toma un systema sys y los parametros de un controlador PD que pueden interpretarse como la posición de una particula; crea el controlador PD realiza la simulación y devuelve los resultados de la simulación.
(define (sim-pd-ctrl sys pos)
(let ([kp (x1-pos pos)]
[kd (x2-pos pos)])
(let ([ ctrl (make-PD kp kd (* kd 10)) ])
(sim-classic-retro sys ctrl))))
Con todos los procedimientos anteriores, ahora se puede construir el procedimiento calc-fitness. Este procedimiento toma la posición de una particula, es decir los parámetros de un controlador, realiza la simulación, a partir de los resultados de simulación construye la señal de error y calcula su norma-dos
(define (calc-fitness pos) (define sal (sim-pd-ctrl sys1 pos)) (define t (vector-map (lambda (v) (vfirst v)) sal)) (define e (vector-map (lambda (v) (- (vthird v) (vsecond v))) sal)) (+ (norm2 (make-dfnc t e))))
El simulador tiene los procedimientos set-interval! y set-dt! para establecer el intervalo de simulación y el paso de integración. Estos procedimientos se deben ejecutar antes de hacer cualquier simulación. En los resultados de esta sección se utilizó
(sim-prmtr 'set-interval! 0.0 16.0) (sim-prmtr 'set-dt! 0.1)
Recuerde que la PSO requiere del problema dos cosas:
- El procedimiento
make-potential-solque crea las particulas al azar. - El procedimiento
calc-fitnessque le asigna una calificación a cada partícula.
Como ya se tienen estos dos procedimientos, lo que resta es decirle al algoritmo en donde encontrar estos procedimientos y ejecutarlo. La siguiente líneas ejecutan la PSO con 10 partículas y 15 iteraciones (movimientos del ejambre). A cada iteración se realizan 10 simulaciones. Así al finalizar la corrida se habrán realizado 150 simulaciones.
;; test pso-data (define datos (make-pso-data 15 10 0.8 0.3 0.4)) (define resultado (pso datos)) (nl) (dp "Resultados:") (display-swarm resultado)
5. Conclusiones
Se ha descrito un programa para implementar el algoritmo de optimización por ejambre de partículas (PSO) usando el lenguaje de programación Racket. El algoritmo se desarrolló de manera bastante general para que con cambios mínimos pueda ser usado en una amplia variedad de problemas. Esto permitió que la aplicación del método a la sintonización de controladores clásicos fuera relativamente sencilla.
Además se describieron las funciones necesarias para extender un simulador desarrollado previamente y poder usar el métodos para sintonizar una variedad de controladores.
Aunque aquí se desarrollaron funciones para sintonizar controladores clásicos aplicados a simtemas líneales, no sería difícil desarrollar funciones para sintonizar controladores más complicados aplicados a sistemas también más complicados.